|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Od mřížových modelů ke kvantové chromodynamice I
Petr Kulhánek
V mnoha případech se vlastnosti magnetických materiálů zkoumají za pomoci tzv. mřížových modelů. Jde o jednoduchý systém, ve kterém jsou ve vrcholech pravidelné mříže lokalizovány magnetické momenty (zpravidla spiny). Ty podle určitého předpisu interagují s nejbližšími sousedy. První takový model vzniknul již v roce 1925. Od té doby se mřížové modely magnetik velmi rozšířily, ukázalo se, že se pomocí nich dá zjišťovat nejen chování různých magnetických materiálů, ale i na první pohled poněkud odlišných systémů, například plynů, plazmatu a nebo chování kvarkůKvarky – částice, ze kterých jsou tvořeny těžké částice s vnitřní strukturou (hadrony). Hadrony dělíme na baryony složené ze tří kvarků (například protony a neutrony) a na mezony tvořené kvarkem a antikvarkem (například piony). Kvarky se dělí do tří generací, první tvoří kvarky „d“ (down) a „u“ (up), druhou kvarky „s“ (strange) a „c“ (charm) a třetí kvarky „b“ (bottom nebo beauty) a „t“ (top nebo truth). Kvarky mají neceločíselné (třetinové a dvoutřetinové) elektrické náboje. Jsou také nositeli barevného náboje silné interakce. uvnitř nukleonuNukleon – společný název pro částice jádra (protony a neutrony). Jde o baryony složené z kvarků „u“ a „d“.. Statistické chování mřížových modelů se velmi často zjišťuje na základě Monte CarloMonte Carlo – skupina numerických metod využívající náhodná čísla a náhodné procesy. Ke nejznámějším patří například Metropolisova metoda. numerických simulacíPočítačová simulace – napodobení skutečnosti pomocí numerického výpočtu, nezbytná součást modelování fyzikálních procesů. Dokáže na základě sofistikovaných algoritmů předpovědět jak kvantitativní, tak kvalitativní výsledky pokusů při různých počátečních podmínkách. Umožňuje omezit výběr jevů, které celý pokus ovlivňují nejvíce, a tím vysvětlit příčiny a podstatu procesů..
|
Feromagnetikum – materiál, ve kterém je energeticky výhodné, aby sousední magnetické momenty měly shodný směr. Tyto látky, například železo, jsou schopné značné magnetizace ve vnějším magnetickém poli. Po odstranění magnetického pole si ponechávají permanentní magnetizaci, tj. zůstávají zmagnetizované i bez vnějšího magnetického pole. Typickým příkladem je krystalické železo, kobalt či oxid chromičitý CrO2. Antiferomagnetikum – systém spinů ve kterém je energeticky výhodné, aby sousední magnetické momenty měly různou hodnotu spinu (například opačný směr). Při nízkých teplotách se vytvářejí periodické struktury opačně orientovaných momentů. Příkladem antiferomagnetika může být supravodič URu2Si2, dále chróm, slitina železa a manganu nebo oxid niklu NiO. Spinové sklo – magnetický materiál, který má za nízkých teplot chaotickou orientaci magnetických momentů. Jejich uspořádání připomíná klasické sklo. Vazbová energie sousedních magnetických momentů se mění náhodně místo od místa. Spin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole. |
Isingův a Pottsův model – nejjednodušší mřížové modely
Nejjednodušší model pochází již z 20. let minulého století. Jde o soustavu spinů na mříži, z nichž každý může mít jen dva stavy (například nahoru a dolů nebo +1 a –1). Dva sousední spiny k celkové energii přispívají hodnotou E = –Js1s2, kde spiny s1 a s2 mohou nabývat +1 nebo –1. Při nízké teplotě jsou preferovány stavy s co možná nejnižší energií, tedy pro J > 0 je preferováno rovnoběžné uspořádání spinů (feromagnetikum) a pro J < 0 střídající se spiny (antiferomagnetikum). Úlohu v jedné dimenzi analyticky vyřešil v rámci své disertační práce Ernst Ising (1900–1998) v roce 1925. Ukázal, že v lineárním řetězci spinů nedochází k žádnému fázovému přechodu. Ve dvou dimenzích (spiny na plošné mříži) nalezl řešení Lars Onsager (1903–1976) v roce 1944. Zde dochází při určité teplotě TC k typickému Courieovu přechodu. Při teplotách nižších než TC se tvoří domény shodně orientovaných spinů. Systém se chová feromagneticky. Při absolutní nule jedna z domén převládne a zaujme celý prostor. Při teplotách vyšších, než je TC, jsou spiny rozmístěny chaoticky a střední magnetizace je velmi nízká. Přechod mezi oběma fázemi má charakter fázového přechodu druhého druhu (k přechodu není třeba latentní teplo, magnetizaceMagnetizace – objemová hustota magnetického dipólového momentu. Jde o vektorový součet všech elementárních dipólových momentů dělený objemem látky. Jsou-li elementární magnety orientovány chaoticky, je výsledná magnetizace nulová. je spojitou funkcí teploty, susceptibilitaSusceptibilita magnetická – změna magnetizace s vnějším magnetickým polem. Pro lineární závislost platí M = χH. V anizotropním prostředí je susceptibilita symetrickým tenzorem druhého řádu. má skok).
Přestože je Isingův model feromagnetik velmi jednoduchý a popisuje feromagnetika jen přibližně, má velký význam jako takový. Snadno lze ukázat, že systém je ekvivalentní statistickému modelu pohybu atomů, ve kterém vrchol mříže buď atom obsahuje, či nikoli (tzv. mřížový plyn). Ze dvou lineárních Isingových řetězců je možné spárovat tzv. kvantový žebřík a studovat na něm uvěznění kvarků, ve vyšších dimenzích je možné simulovat vlastnosti některých typů strunStruny – jednodimenzionální útvary ve vícerozměrném světě (uzavřené nebo otevřené), jejichž vibrační stavy odpovídají jednotlivým elementárním částicím. Jde o podstatný prvek tzv. strunových teorií, které se pokoušejí spojit svět kvantové teorie se zakřiveným prostoročasem obecné relativity. nebo zkoumat vlastnosti renormalizaceRenormalizace – matematická procedura vedoucí k odstranění některých nekonečen vyskytujících se v kvantové teorii. kvantových teorií.
Nejjednodušším zobecněním Isingova modelu je Pottsův model, ve kterém mohou spiny mít Q různých hodnot (mířit Q směry, tzv. Q-stavový model). Interakční předpis pro dva sousední spiny zůstává obdobný, výsledkem je –J, pokud jsou sousední spiny shodně orientované a nula, pokud různě. Opět je tedy při nízké teplotě zjevná preference souhlasných stavů a dochází k tvorbě domén. Za vysokých teplot jsou spiny uspořádány chaoticky, mezi oběma fázemi existuje Curieův fázový přechod, obdobně jako u Isingova modelu. Model je pojmenován podle australského fyzika Renfreye Pottse (1925–2005).

Dvojrozměrný osmistavový Pottsův model, nízkoteplotní fáze s
doménami.
Zdroj: M Kaňok.
Složitější modely
ZQ model
Jedná se opět o Q-stavový dvojrozměrný model, spiny můžeme charakterizovat diskrétními úhly. Interakční energie nejbližších sousedů je dána formulí E = –J cos(α1–α2). Model má pro velká Q tři fáze: Nízkoteplotní uspořádanou fázi s charakteristickými doménami, „soft“ fázi při středních teplotách, při které se sousední spiny svou orientací liší jen velmi málo. Vznikají charakteristické víry spinů nebo spinové vlny. Další fází je vysokoteplotní chaotická fáze. Fázový přechod z nízkoteplotní fáze k „soft“ fázi se nazývá Curieův přechod (TC), fázový přechod ze „soft“ fáze do vysokoteplotní neuspořádané fáze se nazývá Kosterlitzův-Thoulessův přechod (TK). Jde o přechod, při kterém je spojitá susceptibilita (na rozdíl od přechodů druhého druhu). Ke ztrátě kvaziuspořádanosti při přechodu ze „soft“ do chaotické fáze dochází díky příčným fluktuacím neboli tzv. Goldstoneovým modům. Přechod opačným směrem (od neuspořádané ke kvaziuspořádané „soft“ fázi) lze chápat jako narušení rotační symetrie, při kterém se objeví Goldstoneovy mody fluktuací. Přechod je nazván podle amerického fyzika Johna Michaela Kosterlitze a skotského fyzika Davida Thoulesse.

„Soft“ fáze v Z16 modelu. Zdroj: Michal Kaňok.
Heisenbergův model a XY model
Jde o spojité modely které připouštějí veškeré orientace spinů. Energetický předpis je stejný, jako u ZQ modelu, ale spiny mohou mít libovolnou orientaci. Třírozměrná varianta se nazývá Heisenbergův model, dvojrozměrná varianta se nazývá XY model. Modely mají jen dvě fáze: pro nízkoteplotní „soft“ fázi jsou charakteristické dvojice vírů a spinové vlny; vysokoteplotní fáze má spiny orientovány chaoticky. Obě fáze jsou oddělené Kosterlitzovým Thoulessovým přechodem. Materiály popisované Heisenbergovým modelem nemají fázi s doménami. K Heisenbergovým magnetům patří například materiál označovaný GSO s chemickým složením Gd2Sn2O7.

Dvojrozměrný Heisenbergův model, nízkoteplotní „soft“
fáze.
Simulace se 150×150spiny. Zdroj: Michal Kaňok.

Třírozměrný Heisenbergův model, fáze s typickými víry a
spinovými vlnami.
Zdroj: Michal Kaňok.
Spinová skla
Jde o materiály, jejichž magnetické momenty za nízkých teplot „zamrznou“ do náhodných uspořádání. V takovém materiálu neexistuje korelace na velké vzdálenosti. Vazbová konstanta J se liší od dvojice spinů ke dvojici. Často má náhodný charakter. Pro spinová skla je charakeristická existence mnoha metastabilních stavů, jejichž experimentální studium je mimořádně obtížné. Numerické simulace umožňují alespoň rámcové studium těchto zajímavých materiálů. Ke spinovým sklům patří například materiál s chemickým složením LiHoxY1-xF4. Pro vysoký podíl holmia jde o feromagnetikumFeromagnetikum – materiál, ve kterém je energeticky výhodné, aby sousední magnetické momenty měly shodný směr. Tyto látky, například železo, jsou schopné značné magnetizace ve vnějším magnetickém poli. Po odstranění magnetického pole si ponechávají permanentní magnetizaci, tj. zůstávají zmagnetizované i bez vnějšího magnetického pole. Typickým příkladem je krystalické železo, kobalt či oxid chromičitý CrO2., pro x < 0,25 jde o spinové skloSpinové sklo – magnetický materiál, který má za nízkých teplot chaotickou orientaci magnetických momentů. Jejich uspořádání připomíná klasické sklo. Vazbová energie sousedních magnetických momentů se mění náhodně místo od místa.. Magnetické momenty holmiaHolmium – měkký stříbřitě bílý přechodný kovový prvek, 11. člen skupiny lanthanoidů. Nachází využití při výrobě silných permanentních magnetů, speciálních slitin pro jadernou energetiku a při výrobě laserů. Holmium objevili roku 1878 současně Marc Delafontaine, Jacques Louis Soret a Per Teodor Cleve. Holmium je v zemské kůře obsaženo v koncentraci přibližně 1,2 mg/kg. interagují téměř výhradě dipólově, energetický předpis je obdobný Isingovu modelu, ale s chaotickým chováním interakční konstanty. Jiným velice zajímavým materiálem je sloučenina PrAu2Si2. Přestože jde o dobře uspořádanou krystalickou strukturu, při nízkých teplotách vykazuje vlastnosti spinových skel. Mechanizmem vzniku je tzv. dynamická frustrace – jev, při kterém dynamické fluktuace v krystalu znemožní korelace magnetických momentů na větší vzdálenosti. K frustraci dochází tím, že existuje mnoho neslučitelných základních stavů (stavů s nejnižší energií) a jednotlivé silové interakce „soutěží“ o dosažení některého z nich. Výsledkem je vytuhnutí materiálu ve stavu spinového skla s chaotickými vazebními konstantami.
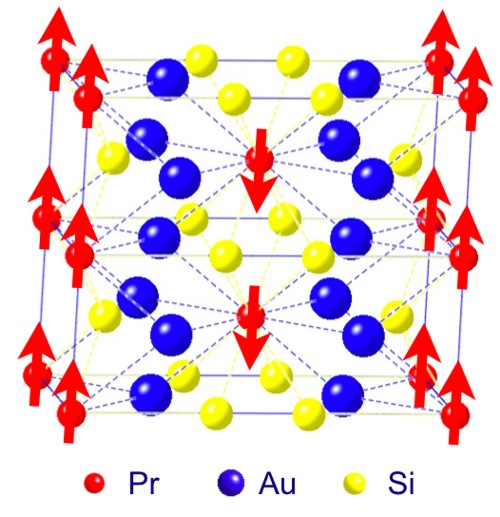
Spinové sklo PrAu2Si2. Červené šipky ukazují směry, kterými by mířily magnetické momenty, pokud by jim dynamická frustrace nezabránila zaujmout krystalickou strukturu. Materiál se při teplotách nižších než 3 K chová jako spinové sklo. Zdroj: Argonne National Laboratory.
Dokončení v čísle 2/2010
Klip týdne: Pottsův model
Pottsův model. Pottsův model patří k mřížovým modelům feromagnetik. Spiny jsou lokalizovány ve vrcholech pravidelné mříže, mohou mít Q stavů s různými směry. K celkové energii systému přispějí hodnotou –J jen nejbližší spiny se souhlasnou orientací. Ostatní konfigurace spinů nepřispějí. Při nízkých teplotách se snaží systém zaujmout co možná nejnižší energii a sousední spiny se snaží být orientovány paralelně. Tím vzniká typická struktura domén se shodně orientovanými spiny. Shodný model se využívá i k simulaci růstu krystalů, namísto spinů máme vhodně orientované krystaly. Animace je výsledkem numerické simulace, která začíná při vysoké teplotě a materiál má chaotické orientace jednotlivých spinů. Se snížením teploty se objeví drobné domény stejně orientovanýczh spinů (jsou označeny stejnou barvou). Při dalším ochlazování dochází k nárůstu velikosti domén. V simulaci šlo konkrétně o růst zrn v měděném nanodrátu popsaném Pottsovým modelem. Zdroj: Matthias Schmidt, Universität Erlangen-Nürnberg. (avi/divx, 1 MB)
Literatura

