|
| |||
|
Týdeník věnovaný aktualitám a novinkám z fyziky a astronomie. | |||
|
Časové krystaly? Utopie se stala realitou
Petr Kulhánek
Krystalickou látku vnímáme jako opakující se periodickou strukturu v prostoru. V roce 2012 přišel americký fyzik Frank Wilczek s fascinující myšlenkou. Nešlo by vytvářet periodické struktury – jakési časoprostorové krystaly – ve všech čtyřech dimenzích? Anebo nebylo by možné vytvořit periodickou strukturu pouze podél časové osy? Tak odvážná předpověď nezůstala bez odezvy ostatních fyziků. Jak už to u každé fascinující myšlenky bývá, fyzikální komunita se rozdělila na dva tábory – nadšené zastánce revolučního nápadu a jeho zavilé odpůrce. Ti brzy přinesli důkaz, že stabilní periodická struktura v čase, která by jevila znaky krystalické látky (tzv. časový krystal), není uskutečnitelná. Zastánci časových krystalů se ale nevzdali a v roce 2016 Norman Yao z Kalifornské univerzity nabídl recept na vytvoření takového krystalu. Předchozí důkaz neexistence byl sice správný, ale týkal se jen látky v termodynamické rovnováze. U nerovnovážného systému je konstrukce časového krystalu možná. Pouhý měsíc po zveřejnění Yaova receptu byl takový krystal zkonstruován a za další měsíc vytvořila časový krystal jiné konstrukce (ale dle stejného receptu) i další skupina. Podivný sen se stal skutečností a tato extravagantní forma látky byla v laboratoři připravena.

Naivní umělecká vize časového krystalu. Jak uvidíme dále, skutečné časové krystaly se od představ autora obrázku značně liší. To ale nic nemění na tom, že obrázek je to zajímavý a snad i trochu tajemný. Zdroj: Garanti.
|
Termodynamická rovnováha – stav systému, při němž neexistují makroskopické toky veličin (přesun náboje, spinu, energie, hmoty atd.) ani v systému samotném, ani mezi systémem a jeho okolím. V systému nenastávají žádné makroskopické změny. Rovnováha se týká tepelných, mechanických, chemických, zářivých a dalších procesů. MBL – Many Body Localized Phase, fáze systému s mnoha tělesy, v níž jsou polohy jednotlivých objektů lokalizovány v určitých místech a tyto polohy jsou stabilní vůči malým vnějším poruchám. Příkladem může být řetězec spinů nebo atomů, v němž má každý z jedinců určitou stabilní polohu. Spin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole. Spintronika – spinová elektronika neboli magnetoelektronika. Jde o technologii využívající kvantové vlastnosti spinu elektronu, případně celého atomu. Zatímco klasická elektronika využívá ve všech technologiích pouze náboj elektronu, ve spintronice se kromě náboje elektronu využívá i orientace jeho spinu. První spintronické logické obvody byly zkonstruovány v roce 1997. |
Wilczekův nápad
Popišme si nejprve jednu důležitou změnu, která nastane při běžné krystalizaci, například vody. V kapalné fázi panuje všesměrová translační symetrie. Budeme-li v rozsáhlé vodní nádrži konat nějaké experimenty, nic se nestane, pokud náš přístroj posuneme v libovolném směru (tíhové pole neuvažujeme). Jakmile ale voda zkrystalizuje, situace se výrazně změní. Objevivší se krystaly vytvoří periodicky se opakující struktury, které naruší translační symetrii. Takové narušení symetrie je pro fázové přechody charakteristické. Přesto není translační symetrie zlikvidována zcela. Stále platí, že pokud se v některých vybraných směrech posuneme o celistvý násobek mřížkové konstanty, nic se nestane. Globální translační symetrie byla narušena a nahradila jí diskrétní translační symetrie. Nemá-li se situace změnit, musíme se posouvat jen po určitých skocích a jen v určitých směrech. Další vlastností krystalické fáze, která stojí za pozornost, je fakt, že periodicita vzniklé krystalické mříže nijak nesouvisí s případnou periodicitou vnějších sil, které ke krystalizaci přispěly, nebo ji dokonce vyprovokovaly.
Frank Wilczek, nositel Nobelovy cenyNobelova cena – je udílena švédskou Královskou akademií věd jednou ročně v pěti kategoriích: za fyziku, chemii, fyziologii a medicínu, literaturu a za úsilí o mír. Cena je hrazena z Nobelovy nadace, kterou založil Alfréd Nobel, vynálezce dynamitu, v roce 1895. První cena za fyziku byla udělena v roce 1901 Wilhelmu Roentgenovi za objev rentgenového záření. Hodnota Nobelovy ceny se mění, v roce 2021 činí 10 milionů švédských korun, tj. 25 milionů českých korun. Uděluje se vždy 10. prosince při výročí smrti Alfreda Nobela. za teorii silné interakceSilná interakce – interakce krátkého dosahu, přibližně 10−15 m. Silná interakce je výběrová, působí jen na částice s barevným nábojem, tj. kvarky. Polními částicemi silné interakce jsou gluony (z anglického „glue“ = lepit, lepidlo). Gluony spojují kvarky do větších celků, tzv. hadronů. Nejznámější jsou proton a neutron složený ze tří kvarků. Silná interakce je odpovědná za soudržnost atomárního jádra. Polní částice mají barevný náboj a proto mohou působit samy na sebe. Barevný náboj na malých vzdálenostech (při vysokých energiích) slábne a kvarky se chovají jako volné částice. Hovoříme o tzv. asymptotické volnosti kvarků. Teorií silné interakce se nazývá kvantová chromodynamika (QCD)., dostal v roce 2012 zajímavý nápad. Nebylo by možné vytvořit periodicky se opakující strukturu v čase, která by narušila globální časovou symetrii a nahradila ji diskrétní časovou symetrií? První, co nás asi napadne, je nějaká soustava pružinek, kterou rozkmitáme vnější silou o určité frekvenci. Ve fyzice tomuto jevu říkáme vynucené kmity. V tomto případě skutečně dojde k narušení globální časové symetrie a situace se při uběhnutí obecného časového intervalu změní. Ke změně nedojde pouze tehdy, posuneme-li se v čase o násobek časové periody kmitů. Doposud to vypadá analogicky jako u prostorové krystalické mříže: globální časová symetrie byla narušena a nahrazena diskrétní časovou symetrií. Naši soustavu pružinek ale rozkmitala vnější síla, která vnutila této soustavě svou frekvenci, a to už si s klasickým krystalem neodpovídá. Mřížková konstanta totiž nijak nesouvisí s periodicitou vnějších podnětů. Na časové krystaly tedy budeme klást dva požadavky: 1) musí jít o děj periodický v čase, který naruší globální časovou symetrii a nahradí ji diskrétní časovou symetrií, tj. systém se po určité době vrátí do původního stavu; 2) periodicita děje nesmí být shodná s periodicitou jakékoli vnější síly, která pohyb způsobila. Naše soustava pružinek nesplňuje druhou vlastnost, a časovým krystalem proto není.
Existuje ale jiný myšlenkový experiment, který splňuje obě vlastnosti časového krystalu. Představme si lineární řetězec malých elementárních magnetů, například spinůSpin – vlastní (vnitřní) rotační moment částice souvisící s Lorentzovou symetrií. Pro částici v centrálním poli se přirozeným způsobem skládá s momentem hybnosti. Částice s nenulovým spinem se mohou chovat jako elementární magnetické dipóly μ, aniž by měly elektrický náboj. Takové částice reagují na vnější magnetická pole. (ty mohou být reprezentovány nějakými vhodnými atomy). Předpokládejme, že máme k dispozici laserLASER – Light Amplification by Stimulated Emission of Radiation, zesílení světla pomocí stimulované emise záření. Roku 1958 ukázal Charles Hard Townes spolu s Arthurem Leonardem Schawlowem, že je možné zkonstruovat podobné zařízení jako již existující MASER (pracuje v mikrovlnné oblasti) také pro světlo. První laser zkonstruoval Theodore Harold Maiman v roce 1960. Aktivním prostředím byly ionty chrómu v syntetickém rubínovém krystalu., jehož impulz dokáže všechny spiny otočit do opačného směru. Tímto laserem budeme na náš řetězec spinů pravidelně vysílat jeden impulz za druhým. Periodicitu vysílaných impulzů označíme T. Po čase T budou mít všechny spiny opačný směr, po čase 2T bude jejich směr stejný, jako tomu bylo na počátku atd. Naše spiny se budou pravidelně přetáčet sem a tam a zjevně naruší globální časovou symetrii. Celá perioda překlápění spinů bude 2T, což odpovídá poloviční frekvenci vysílaných impulzů (hovoříme o první subharmonické frekvenciSubharmonická frekvence – frekvence, která je celočíselným zlomkem původní frekvence, tedy její polovina, třetina, čtvrtina atd. Opakem je harmonická frekvence, která je celistvým násobkem původní frekvence.). Takové rozkývané spiny splňují obě části definice časového krystalu. Globální časová symetrie je nahrazena diskrétní časovou symetrií (s periodicitou 2T) a systém kmitá na subharmonické frekvenci řídících impulzů, tedy na frekvenci, která není totožná s frekvencí vnějších podnětů. Je tedy toto časový krystal? Bohužel není, neboť situace je značně nestabilní a energie, kterou dodávají do systému vnější impulzy, bude řetězec atomů rychle zahřívat nade všechny meze a jakékoli periodické překlápění téměř okamžitě vymizí. Takový systém není v termodynamické rovnováze a přebírá z okolí značnou energii. Zanedlouho po publikaci Wilczekova nápadu s časovými krystaly byl podán důkaz, že takový krystal nemůže nikdy existovat v termodynamické rovnováze s okolím a zdálo se, že je smělá myšlenka odsunuta kamsi do hlubin říše naší fantazie.
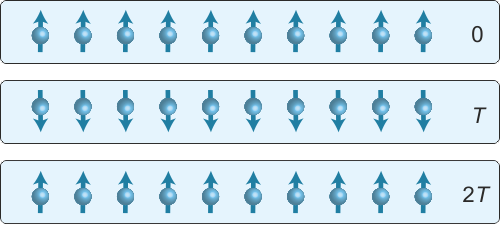
Periodicita impulzů, které přetáčejí spiny, je T, periodicita pohybu samotných spinů je 2T. Takový systém vstřebává energii z vnějších podnětů, bude se intenzívně zahřívat a po krátké době přestanou být spiny lokalizovány ve svých polohách. Kresba autor.
Yaův recept
V srpnu 2016 zveřejnil americký fyzik Norman Yao z Kalifornské univerzity postup, jak by bylo možné vyrobit časový krystal, který nebude v termodynamické rovnováze [2]. Učinil tak prostřednictvím archivu volně dostupných článků Cornellovy univerzity. K publikaci v recenzovaném periodiku (Physical Review Letters) došlo paradoxně až 17. ledna 2017, tj. poté, co byly dle jeho postupu časové krystaly připraveny. A jaký je tedy recept na časový krystal? Výše uvedený příklad s překlápěním spinů je možné zdokonalit přidáním dalších dvou fází. V první fázi za pomoci laserového impulzu otočíme spiny o určitý úhel, ideálně o 180°, tedy ?. Tato první operace bude trvat T1 a nikdy nebude zcela ideální. Skutečný úhel otočení se od požadované hodnoty ? může poněkud lišit, označme ho ? = ?(1-?). Parametr ? charakterizuje nepřesnost realizace první fáze (překlopení spinu). V druhé fázi trvající T2 iniciujeme vzájemnou interakci spinů mezi sebou. Může jít jen o interakci mezi nejbližšími spiny, jak je tomu v klasickém Isingově modelu (viz [10]), interakce ale může probíhat podle určitého předpisu i mezi vzdálenějšími spiny. Intenzitu interakce charakterizuje určitá vazbová konstanta J. Poslední, třetí fáze, trvá dobu T3 a vnáší do systému chaos. To lze realizovat například chaotickým magnetickým polem. Tyto tři fáze se neustále opakují, řídící (vnější proces má tedy periodu T = T1 + T2 + T3. Periodicita překlápějících se spinů bude opět 2T. V původním Yaově návrhu byly fáze 2 a 3 spojené do jedné jediné.
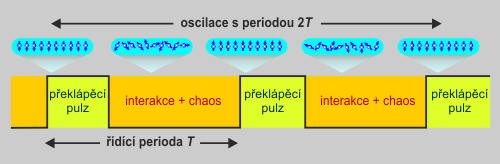
Původní Yaův návrh obsahoval jen dvě fáze: 1) překlápění spinů
2) jejich vzájemnou
interakci doprovázenou chaotickým působením magnetického
pole. Zdroj: [6]
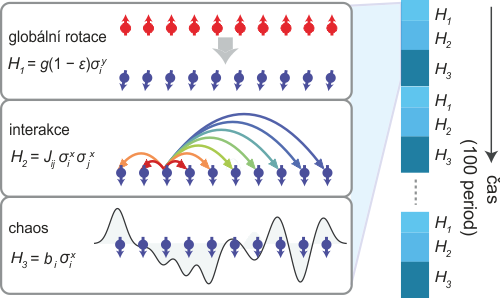
Zanedlouho byl „recept“ na časový krystal zdokonalen. Exotický krystal je možné vytvořit neustálým opakováním tří základních dějů: 1) překlopení spinů, 2) vzájemná interakce spinů, 3) vliv chaotického pole. Vztahy uvedené v obrázku charakterizují energetickou bilanci jednotlivých procesů. Zdroj: [3].
Norman Yao ukázal, že vzájemná interakce a chaotické působení budou časový krystal stabilizovat. Za přítomnosti těchto dějů nedojde k zahřívání krystalu a pro určité oblasti parametrů skutečně vznikne MBL fázeMBL – Many Body Localized Phase, fáze systému s mnoha tělesy, v níž jsou polohy jednotlivých objektů lokalizovány v určitých místech a tyto polohy jsou stabilní vůči malým vnějším poruchám. Příkladem může být řetězec spinů nebo atomů, v němž má každý z jedinců určitou stabilní polohu. s narušením globální časové symetrie a nastolením diskrétní časové symetrie – tedy časový krystal vykonávající kmity na subharmonických frekvencích. Yao odvodil i jednoduchý fázový diagram odpovídající jeho „receptu“ na časový krystal. Yaovy vazby na další pracoviště umožnily následnou „výrobu“ časového krystalu, a to hned na dvou místech. Norman Yao byl u obou experimentů, a je tak nejenom autorem receptu na časový krystal, ale i spoluautorem obou stěžejních experimentů. Můžeme tedy říci, že Frank Wilczek je duchovním otcem časových krystalů a Norman Yao je jejich „biologickým“ otcem.
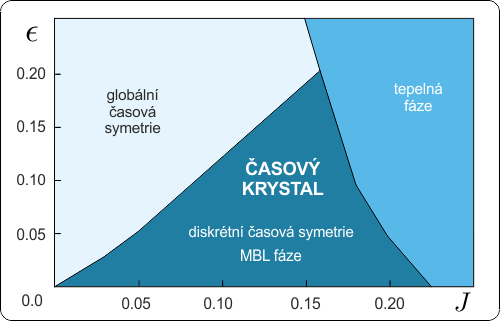
Na svislé ose je parametr ? charakterizující nepřesnost překlopení spinů. Na vodorovné ose je vazebná konstanta vzájemné interakce spinů. V určité oblasti parametrů se skutečně objeví časový krystal s diskrétní časovou symetrií, v němž jsou spiny stabilně lokalizovány ve svých polohách (tzv. MBL fázeMBL – Many Body Localized Phase, fáze systému s mnoha tělesy, v níž jsou polohy jednotlivých objektů lokalizovány v určitých místech a tyto polohy jsou stabilní vůči malým vnějším poruchám. Příkladem může být řetězec spinů nebo atomů, v němž má každý z jedinců určitou stabilní polohu.). Nakresleno podle [2].
Máme je – první časové krystaly
První časový krystal byl podle Yaova receptu připraven v září 2016, pouhý měsíc po jeho zveřejnění. Podařilo se to skupině Chrise Monroea z Marylandské univerzity [3]. K „výrobě“ využili deset ytterbiovýchYtterbium – měkký stříbřitě bílý, přechodný kovový prvek, 14. člen skupiny lanthanoidů. Ytterbium objevil roku 1878 švýcarský chemik Jean Charles Galissard de Marignac. Ytterbium se vyskytuje v zemské kůře v koncentraci 3 mg/kg. iontů, z nichž vytvořili lineární řetězec držený v Paulově radiofrekvenční pastiPaulova past – třírozměrná verze kvadrupólových elektrických polí generovaných speciální konfigurací elektrod. Pole mění svou polaritu většinou na radiové frekvenci a ve středu zařízení udržuje shluk iontů. Paulova past se používá v hmotových spektrometrech a při realizaci kvantových počítačů. Je pojmenována po německém fyziku Wolfgangu Paulovi, který za její konstrukci získal Nobelovu cenu za fyziku v roce 1989.. Překlápění spinů způsobil elektromagnetický impulz v optické oblasti generovaný Ramanovým laseremRamanův jev – také Ramanův rozptyl (kombinační rozptyl, Mandelstamův rozptyl, Smekalův-Ramanův rozptyl). Jde o změnu směru i velikosti vlnového vektoru a polarizace fotonů při průchodu prostředím v důsledku interakce s dvěma stavy atomu či molekuly. Rozptýlené fotony mají jinou frekvenci, fázi i polarizaci a nesou informace o energetickém spektru rozptylového centra a u molekul dokonce i o prostorové orientaci konkrétní chemické vazby, tedy jakési molekulární „vizitky“. Pokud má rozptýlený foton nižší energii než původní, hovoříme o tzv. Stokesově fotonu. Bez speciálních opatření je však tímto způsobem rozptylován pouze jediný foton ze stovek miliónů až stovek miliard dopadajících fotonů. Účinný průřez Ramanova rozptylu je zhruba 10−30 cm2. Pokud do prostředí posíláme fotony s vhodnou frekvencí, může dojít ke stimulovanému Ramanovu rozptylu, který je mnohem účinnější. Na tomto jevu jsou založeny Ramanovy lasery.. Druhá fáze, tj. interakce spinů, byla vyprovokována spinově závislými dipólovými silami v optické oblasti. A poslední, třetí fáze týkající se chaosu, byla implementována optickými poli laserového svazku, který byl přesně fokusován na jednotlivé ionty. Tyto tři fáze trvaly zhruba 75 mikrosekund a byly opakovány řádově stokrát. Přitom byla měřena magnetizace (průměrný magnetický moment) každého jednotlivého iontu vytvořeného lineárního řetězce (viz následující obrázek). Zaznamenaná data byla podrobena frekvenční analýze, ze které se ukázalo, že systém při určité hodnotě parametrů osciluje dominantně na polovině řídící frekvence (ta je dána trváním všech tří fází spinové manipulace), a je tedy skutečně časovým krystalem.
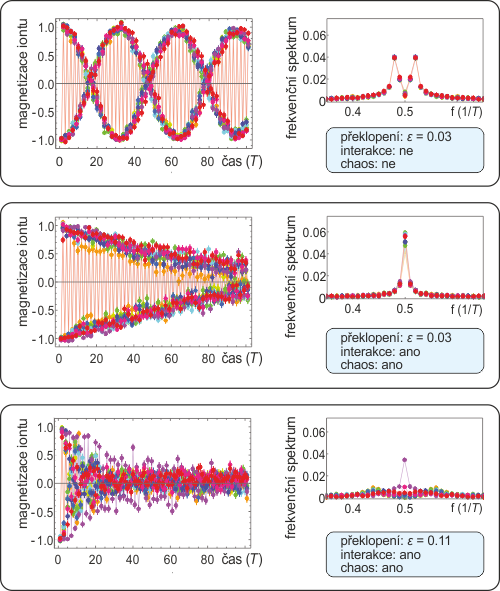
Výsledky měření magnetizace konkrétního iontu. Napravo je pro každý případ zobrazen výsledek frekvenční analýzy vyprovokovaných oscilací. V prvním případě (bez interakční a chaotické fáze) je pík na poloviční frekvenci rozštěpen, systém je nestabilní a absorbuje energii zvnějšku. Druhý případ (s chaotickou i interakční fází) je ideální, frekvence f0/2 má ostrý pík. Ve třetím případě je ? = 0,11, tj. fáze překlápění je nastavena dosti nepřesně. Za následek to má výrazné snížení rezonančního píku na subharmonické frekvenci f0/2.
O pouhý měsíc později, v říjnu 2016, byl dle stejného receptu připraven časový krystal zcela jiné konstrukce. Podařilo se to skupině z Harvardu vedené Michailem Lukinem. K experimentům použili diamantový krystal, do něhož za pokojové teploty záměrně zanesli zhruba milión nečistot – dvojice uhlíkových atomů nahradili dusíkem a nezaplněným místem (vakancí). Takto vzniklá dipólová centra se opět chovají jako elementární spiny (magnety), s nimiž lze manipulovat podobně jako s ytterbiovým řetězcem. Jediným větším rozdílem je to, že v tomto případě vše probíhá nikoli v optické oblasti, ale v mikrovlnném oboru. Skupině se opět podařilo připravit časový krystal, v němž vyprovokovali oscilace na subharmonických frekvencích f0/2 a f0/3. Podrobný popis výsledků tohoto experimentu najde čtenář v článku [4].
Závěr
Po zveřejnění postupu, jak by bylo možné časový krystal vytvořit, se velmi rychle objevily hned dva způsoby získání časového krystalu. Z toho lze usoudit, že příprava zcela nového exotického stavu hmoty je technologicky relativně snadno zvládnutelná. Časové krystaly narušují globální časovou symetrii a nastolují diskrétní časovou symetrii systému. Ukázalo se, že není možné je připravit v termodynamické rovnováze s okolím. Další zajímavostí je, že je časový krystal ve stavu věčného pohybu, kmitá na subharmonických frekvencích vzhledem k vnějším podnětům. Pokud mají spiny dva základní stavy lišící se pouze opačnou orientací spinu, je teoreticky možné vyprovokovat neustálé překlápění mezi těmito dvěma stavy i bez dalších vnějších podnětů. Na první pohled to zní jako perpetuum mobile – splnění dávného snu o věčném pohybu. Z takového překlápění ale nelze energii nijak získat, oba stavy mají nejnižší možnou energii a jde o základní stavy systému. Naopak: abychom tento pohyb zastavili, musíme do systému dodat nenulovou energii. Jinou variantou „věčného“ pohybu je kroužení. Představme si jehlu postavenou na špičce. Ta může spadnout kterýmkoli směrem, čímž získá nejnižší možnou energii a současně dojde k narušení symetrie (z mnoha směrů byl vybrán jeden jediný). Pokud by nešlo o jehlu na podložce, ale o kvantový systém, mohla by se taková „kvantová jehla“ začít otáčet na desce stolu. Všechny její polohy by totiž měly nejnižší možnou energii (samozřejmě u skutečné jehly tomu zabrání tření). Ve světě spinů můžeme na obdobném principu vytvořit kroužek rotujících spinů. Z takového pohybu opět nelze energii získat, takže o perpetuum mobile v klasickém smyslu nejde. K zastavení pohybu je třeba opět dodat určitou energii. Časové krystaly jsou velmi zajímavou formou hmoty a lze očekávat jejich neméně zajímavé aplikace. V současnosti se hovoří o možné konstrukci nového typu počítačových pamětí založených právě na časových krystalech. Časové krystaly se také mohou stát ústřední komponentou usilovně vyvíjených kvantových počítačů. Žijeme v převratné době a další aplikace na sebe jistě nedají dlouho čekat.
Experiment na Harvardu.
Do diamantu jsou implementována spinová centra,
se kterými se manipuluje ve
dvou fázích. Zdroj: [4].
Odkazy
- Frank Wilczek: Quantum Time Crystals; Physical Review Letters 109/16 (2012)
- N. Y. Yao et al.: Discrete Time Crystals: Rigidity, Criticality, and Realizations; Physical Review Letters 118 (2017) 030401
- J. Zhang et al.: Observation of a Discrete Time Crystal; arXiv:1609.08684 27 Sep 2016
- Soonwon Choi et al.: Observation of discrete time-crystalline order in a disordered dipolar many-body system; arXiv:1610.08057, 25 Oct 2016
- Bec Crew: Physicists Just Created the World's First Time Crystal; Science Alert, 7 Oct 2016
- Phil Richerme: Viewpoint – How to Create a Time Crystal; Physics, 18 Jan 2017
- Robert Sanders: Scientists unveil new form of matter: time crystals; Berkeley News, 26 Jan 2017
- David J. Luitz, Nicolas Laflorencie, Fabien Alet: Many-body localization edge in the random-field Heisenberg chain; Phys. Rev. B 91 (2015) 081103
- Wikipedia: Space-time crystal
- Petr Kulhánek: Statistická fyzika; AGA 2016
- Stanislav Mihulka: Vědci stvořili časové krystaly a zároveň novou formu hmoty; OSEL 29. ledna 2016