Fyzika 1 semináře, zimní semestr 1999/00 zadání testů
Zadání příkladů v seminárních testech
Fyzika 1 semináře, letní semestr 1999/00
Cvičící : Martin Žáček
| Poř. |
Zadání |
|
1
|
Automobil se pohybuje se zrychlením a = -2 m/s2 . Počáteční rychlost automobilu je v0 = 72 km/h.
a) Za jak dlouho se zastaví? (3 body)
b) Jakou urazí dráhu? (3 body)
c) Jaká brzdící síla musí působit na automobil, je-li jeho hmotnost m = 500 kg? (2 body) |
[a) t = 10 s; b) s = 100 m; c) F = 1000 A]
|
2
|
Těleso vystřelíme svisle vzhůru rychlostí v0 = 100 m/s.
a) Jaká bude rychlost tělesa za dobu 3 s? (3 body)
b) Jaká bude maximální výška tělesa? (3 body)
c) Za jak dlouho dopadne těleso zpět na zem? (2 body)
Gravitační zrychlení uvažujte g = 10 m/s2. Odpor vzduchu zanedbejte.
[a) v(t = 3 s) = 70 m/s; b) hmax = 500 m; c) t = 20 s]
|
|
3
|
Do studny pustíme kamínek. Dopad do vody uslyšíme za 4 sekundy (zpoždění v důsledku konečné rychlosti zvuku a odpor vzduchu zanedbejte).
a) Jak hluboká je studna? (2 body)
b) Jakou rychlostí kamínek dopadl? (3 body)
c) Jakou rychlost měl kamínek v polovině dráhy? (3 body)
Gravitační zrychlení uvažujte g = 10 m/s2
[a) h = 80 m; b) v = 40 m/s; c) v1 = 28,3 m/s]
|
|
4
|
a) Napište (vektorovou) pohybovou rovnici pro těleso pohybující se volně v homogenním gravitačním poli v malé výšce nad zemským povrchem. Uvažujte dvě dimenze, souřadnice x je rovnoběžná se zemským povrchem, souřadnice y směřuje kolmo vzhůru. (4 body)
b) Napište obecné řešení těchto pohybových rovnic. (4 body)
[a) po složkách: 0 = m.ax, -mg = m.ay, ve vektorovém tvaru: (0, -mg) = m. (ax, ay) ; b) x(t) = vx0t + x0, y(t) = -1/2 gt2 +vy0t + y0]
|
|
5
|
Těleso vyhodíme kolmo vzhůru rychlostí v0= 10 m/s. Odpor vzduchu zanedbejte.
a) Napište závislost výšky tělesa na čase. (3 body)
b) Za jak dlouho se bude nacházet ve výšce h = 3,2 m nad zemským povrchem? (najděte všechna řešení) (3 body)
c) Za jak dlouho těleso dopadne zpět na zem?(2 body)
Gravitační zrychlení uvažujte g = 10 m/s2.
[a) y(t) = -gt2/2 + v0t; b) t1 = 0,4 s; t2 = 1,6 s; c) t2 = 2 s]
|
|
6
|
a) Z jaké výšky musíme pustit kámen, aby dopadl na zemský povrch za čas t = 2 s? (3 body)
b) Jakou rychlost bude mít v okamžiku dopadu? (3 body)
c) Jakou rychlost bude mít kámen po uražení jedné čtvrtiny celkové dráhy? (2 body)
Zanedbejte odpor vzduchu a gravitační zrychlení uvažujte g = 10 m/s2.
[a) h = 20 m; b) v = 20 m/s2; c) v1 = 10 m/s2]
|
|
7
|
Těleso se pohybuje rovnoměrně zpomaleně, zastaví se během deseti sekund a urazí dráhu 100 m.
a) Jaké je zrychlení tělesa? (3 body)
b) Jaká byla rychlost tělesa na počátku? (3 body)
c) V jakém místě dráhy bude mít právě poloviční rychlost v porovnání s rychlostí na začátku? (2 body)
[a) a = -2 m/s2; b) v0 = 20 m/s; c) s1 = 75 m]
|
|
8
|
Přes nehmotnou kladku upevněnou na siloměru visí nehmotné lano, na jehož koncích jsou připevněna závaží o hmotnosti m1 = 1 kg a m2 = 2 kg.
a) Napište pohybovou rovnici. (4 body)
b) Jakou sílu ukáže siloměr, nechají-li se závaží na kladce volně pohybovat?. (4 body)
[a) (m1 - m2)g = (m1 + m2)a; b) F = 2T = 4g(m1m2)/(m1 + m2) = 80/3 A]
|
|
9
|
Přes pevnou kladku visí nehmotné lano, na jehož koncích jsou připevněna závaží o hmotnosti m1 a m2.
a) Napište pohybovou rovnici. (4 body)
b) Jakou silou je napínáno lano? (4 body)
[a) (m1 - m2)g = (m1 + m2)a; b) F = 2g (m1m2/(m1 + m2)]
|
|
10
|
Po půlkuhové rampě tvaru U necháme volně bez tření klouzat těleso o hmotnosti m = 1 kg z výšky R = 5 m s nulovou počáteční rychlostí. R je poloměr kruhového oblouku rampy.
a) Jakou rychlostí se těleso bude pohybovat v nejnižším bodě? (4 body)
b) Jakou silou bude těleso působit na podložku v nejnižším bodě? (4 body)
[a) v =10 m/s; b) F = 30 N]
|
|
11
|
Automobil o hmotnosti m = 250 kg se pohybuje po rovné silnici, bez tření, vlastní sestrvačností stálou rychlostí v = 20 m/s. Přejede klenutý most, jehož převýšení je h = 12,2 m a poloměr kruhového oblouku mostu je R = 50 m.
a) Jakou rychlostí se automobil bude pohybovat v nejvyšším bodě mostu? (4 body)
b) Jakou silou bude automobil působit na most v nejvyšším bodě? (4 body)
Zanedbejte všechny ztráty třením a gravitační zrychlení uvažujte g = 10 m/s2.
[a) v2= sqrt(156) m/s = 12,5 m/s; b) F= 1720 N]
|
|
12
|
a) Na rovníku vyhodíme kamínek do výšky a necháme ho dopadnout zpět na zem. Kterým směrem se odchýlí bod dopadu v důsledku Coriolisovy síly?
Odpověď (2 body) , vysvětlení (2 body) .
Návod: Porovnejte tangenciální složku rychlosti vzhledem k zemské ose v každém bodě dráhy s případem, kdyby se kamínek pohyboval přesně po svislici.
b) Kterým směrem by se kamínek odchýlil, nechali-li bychom ho padat volným pádem s nulovou počáteční rychlostí? (rovněž na rovníku)
Odpověď (2 body) , vysvětlení (2 body) .
[a) Odchýlí se na západ, kamínek si udržuje setrvačností obvodovou rychlost odpovídající zemskému povrchu na rovníku, aby byl stále nad stejným bodem zemského povrchu, musela by jeho obvodová rychlost růst, proto se za zemským povrchem spozdí.
b) Zde to bude naopak, kamínek si po celou dobu pádu udržuje setrvačností tangenciální rychlost vůči zemské ose odpovídající jeho nejvyšší poloze. Ta je vždy vyšší, než obvodová rychlost bodu svislice, který kamínek právě míjí, a proto se "předběhne" na východ. Tentýž výsledek dostaneme z vektorového součinu v'xw.]
|
|
13
|
Na kolotoči tvaru vodorovné kruhové desky otáčející se rychlostí 1 otáčka za 20 s, se pohybuje člověk o hmotnosti m = 80 kg v radiálním směru rychlostí 1 m/s
a) Nakreslete obrázek s vyznačením vektoru úhlové rychlosti w, vektoru obvodové rychlosti člověka, vektoru lokální rychlosti v' a vektoru Coriolisovy síly. (4 body, za každý správný vektor jeden bod )
b) Vypočtěte velikost Coriolisovy síly podle vzorce Fc = 2mv'xw. (4 body)
[a) Vektor w je kolineární s osou otáčení, orientace se určí podle pravidla šroubu či vývrtky, podle toho, je-li student zaměřen spíše na techniku nebo na alkohol. Vektor v' je přímo zadán, obvodová rychlost je kolmá na v' a míří ve směru otáčení, Coriolisova síla má opačný směr než obvodová rychlost;
b) F = 4pmv'/T = 16p A]
|
|
14
|
Závaží o hmotnosti m1 klouzající s nulovým třením po vodorovné desce je spojeno lanem s druhým tělsem o hmotnosti m2, visícím přes kladku upevněnou na okraji desky.
a) Napište pohybovou rovnici soustavy obou těles. (3 body)
b) Jaké bude zrychlení soustavy, necháme-li soustavu těles volně pohybovat, bude-li hmotnost tělesa klouzajícího po vodorovné desce m1 = 2 kg a hmotnost visícího tělesa m2 = 1 kg? (3 body)
b) Jaký by musel být koeficient tření mezi tělesem a deskou, aby se soustava nepohybovala? (2 body)
[a) m2g = (m1 + m2)a; b) a = m2/(m1 + m2) g = 1/3 g; c) f = m2/m1 = 1/2]
|
|
15
|
Po nakloněné rovině s úhlem sklonu 30o se pohybuje těleso s počáteční rychlostí v0 = 10 m/s směrem největšího stoupání. Koeficient tření mezi tělesem a rovinou je f = 0,5.
a) Napište pohybovou rovnici. (2 body)
b) Jaké bude zrychlení tělesa? (3 body)
c) Do jaké maximální výšky těleso vystoupí? (3 body)
Gravitační zrychlení uvažujte g = 10 m/s2, sin 30o = 0,5, cos 30o = 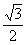 . .
[a) ma = mg sina + mgf cosa;
b) a = g(1 + f)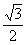 = 15 = 15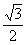 m/s2; c) h = v02/(2g(1 + f m/s2; c) h = v02/(2g(1 + f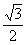 )), přibližný numerický výsledek: h = 2,68 m] )), přibližný numerický výsledek: h = 2,68 m]
|
|
16
|
Těleso o hmotnosti 1 kg klouže po vodorovném povrchu bez tření rychlostí v = 4 m/s, narazí do stojícího tělesa o hmotnosti 2 kg. Po nárazu bude mít první těleso rychlost opačně orientovanou o velikosti v1 = 1 m/s.
a) Napište správně všechny zákony zachování. (2 body)
b) Jakou rychlostí v2 se bude pohybovat druhé těleso po srážce? (3 body)
c) Jaká energie připadne na ztráty způsobené ohřátím těles, deformací ap? Půjde o dokonale pružnou srážku? Bude takto zadaná srážka možná? (3 body, bod za každou správnou odpověď)
[a) mv = m1v1+m2v2, zákon zachování kinetické energie obecně platit nemusí ; b) v = 5/2 m/s; c) Eztráty = 5/4 J, srážka nebude dokonale pružná, srážka je možná]
|
|
17
|
Těleso o hmotnosti 2 kg klouže po vodorovném povrchu bez tření rychlostí v1 2 m/s, narazí do tělesa o hmotnosti 1 kg pohybující se ve stejném směru rychlostí v2 = 1 m/s. Srážka je dokonale pružná.
a) Napište správně všechny zákony zachování. (2 body)
b) Jakou rychlostí u1 a u2 se budou pohybovat obě tělesa po srážce? (4 body)
c) Jaká bude orientace rychlosti narážejícího tělesa? Odrazí se, nebo se jen zpomalí? (2 body)
[a) 5 kgm/s = 2v1 + v2, 9/2 J = v12 + 1/2 v22; b) v1 = 4/3 m/s, v2 = 7/3 m/s; c) Rychlost prvního tělesa se pouze zmenší ze 2 m/s na 4/3 m/s, po srážce se bude pohybovat ve stejném směru jako před srážkou.]
|
|
18
|
Na nehmotném nosníku délky l, podepřeném na obou koncích tak, aby nosník byl ve vodornovné poloze, jsou položena dvě závaží, první o hmotnosti 5 kg ve vzdálenosti 1/5 l od levé podpěry, druhé o hmotnosti 1 kg ve vzdálenosti 3/4 l od levé podpěry.
a) Nakreslete všechny síly působící na soustavu nosník + závaží. (2 body)
b) Napište podmínky rovnováhy pro soustavu nosník + závaží. (3 body)
c) Jakými silami budou na nosník působit obě podpěry? (3 body)
Gravitační zrychlení uvažujte g = 10 m/s2.
[a) celkem 4 síly, F1 a F2 míří vzhůru a působiště mají na obou koncích nosníku, síla 50 N působí v jedné pětině nosníku a síla 10 N ve 3/4 délky nosníku; b) F1 + F2 - 10 - 50 = 0; 1/5*5g + 3/4*g - F1 = 0; c) F1 = 17/4 g, F2 = 7/4 g]
|
|
19
|
Tyč o hmotnosti m a délky l je opřena o stěnu a podlahu tak, že úhel mezi tyčí a podlahou je 60o. Mezi tyčí a stěnou nedochází ke tření, mezi tyčí a podlahou ke tření dochází.
a) Nakreslete všechny síly působící na tyč. (2 body)
b) Napište podmínky rovnováhy. (3 body)
c) Je-li zadána tíha tyče G, jakou velikost budou mít všechny ostatní síly?(3 body)
cos 60o = 0,5, sin 60o = 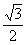
|
|
20
|
Dva hmotné body o hmotnostech m1 a m2 pohybující se proti sobě narazí na sebe. Kinetická energie druhého bodu je 4krát větší než kinetická energie prvního. Dojde k dokonale nepružnému rázu, přičemž vznikne nový hmotný bod o hmotnosti m1 + m2.
a) Napište správně všechny zákony zachování. (2 body)
b) Jakou rychlostí v se hmotné body budou pohybovat po srážce? (2 body)
c) Za jaké podmínky se hmotné body budou po srážce pohybovat ve směru hmotného bodu s nižší energií před srážkou? (2 body)
d) Jaká část původní kinetické energie obou hmotných bodů se změní v tepelné ztráty? (2 body)
[a) m1v1 - m2 v2 = (m1 + m2)v; 6*1/2 m1v12 = 1/2 (m1 + m2)v2 + Q kde Q je ztrátová energie; b) v = (m1v1 - m2 v2)/(m1 + m2); c) 4m1 > m2; d) 2*sqrt(m1m2)/(m1 + m2)]
|
|
21
|
Lampa je zavěšena na stěnu tak, že visí na konci homogenní vodorovné tyče, jejíž druhý konec se opírá kolmo o stěnu. Tyč je držena ve vodorovném směru lanem uchyceném mezi jedním koncem tyče a stěnou nad lampou tak, že svírá s vodorovným směrem úhel 45o (viz obrázek na tabuli).
a) Nakreslete všechny síly působící na tyč. (3 body, za každou chybějící sílu nebo sílu navíc o jeden bod méně)
b) Napište podmínky rovnováhy pro tyč. (3 body)
c) Jakou sílou působí na tyč lano? (1 bod)
d) Jakou sílou působí kolmo na tyč stěna? (1 bod)
[a) Na tyč bude působit 5 sil, stěna působí kolmou silou F1 a podélnou třecí silou F2, lano působí silou F3, na tyč působí tíha G1 a lampa působí na tyč tíhou G2;
b) S označením totožným podle a) a s volbou vztažného bodu v místě upevnění lampy budou mít podmínky rovnováhy tvar: F1 = F3/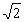 F2 = F3/
F2 = F3/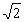 = G1 + G2;
l*G1/2 = F2*l kde l je délka tyče;
c) F3 = = G1 + G2;
l*G1/2 = F2*l kde l je délka tyče;
c) F3 = 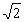 (G1/2 + G2)
d) F1 = F3/ (G1/2 + G2)
d) F1 = F3/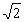 = G1/2 + G2] = G1/2 + G2]
|
|
22
|
Jsou dány 3 hmotné body o hmotnostech m1 = 1 kg, m2 = 2 kg a m3 = 3 kg, jejichž polohové vektory jsou v kartézských souřadnicích x,y,z r1 = (1, 3, 4) m, r2
= (1, 1, 2) m a r3 = (4, 0, 4) m.
Spočítejte polohový vektor těžiště. (5 bodů)
"Záchranná otázka:" Najděte souřadnice těžiště yT a zT grafickým řešením v rovině YZ. (3 body)
[rT = (15, 5, 20)/6 m]
|
|
23
|
Homogenní koule má moment setrvačnosti vzhledem k ose procházející jejím středem
J =2/5 mR2, kde R je poloměr koule a m je její hmotnost.
a) Pomocí Steinerovy věty spočítejte moment setrvačnosti výstředně upevněné
koule pomocí nehmotného ramene délky R (délka je počítána od povrchu koule).
(4 body)
b) Porovnejte moment setrvačnosti získaný podle bodu a) s momentem setrvačnosti pro případ,
nahradíme-li kouli hmotným bodem ležícím ve středu koule.
(4 body)
[a) J = 22/5 mR2; b) J2 = 4 mR2 < J]
|
|
24
|
Homogenní tyč se otáčí kolem osy kolmé na tyč, vzdálenost bližšího konce od
osy je stejná jako délka tyče a je rovna l. Hmotnost tyče je m.
a) Integrací vypočítejte moment setrvačnosti tyče. (4 body)
b) Vypočítejte tentýž moment setrvačnosti pomocí Steinerovy věty, víte-li, že
moment setrvačnosti vzhledem k ose procházející jejím středem J = 1/12 ml2. (2 body)
c) Porovnejte předchozí hodnotu momentu setrvačnosti s případem, kdy otáčející tyč bude rovnoběžně s osou otáčení při stejné vzdálenosti těžiště tyče od osy. (2 body)
[a), b) J = 7/3 ml2; c) J2 = 3/2 mi2 < J]
|
|
25
|
Délka tyče o průřezu S = 1 cm2 při natahování silou F = 100 N je l = 1,26 m. Youngův modul pružnosti je E = 2.107 N/m2.
a) Vypočítejte klidovou délku tyče l0. (5
bodů)
b) Určete relativní deformaci e. (3 body)
[l0 = 1,2 m; e = 0,05]
|
|
26
|
Vodorovná trubice o různých průřezech je protékána vodou. Proudění je laminární a vnitřní tření vody lze zanedbat. V místě průřezu S1
= 30 cm2 je rychlost vody v1 = 5 m/s a tlak P1 = 2.105
Pa. Tlak v jiném místě trubice je P2 = 1.105 Pa.
a) Napište vztah mezi tlakem a rychlostí v trubici. (2 body)
b) Spočítejte rychlost v2. (3 body)
c) Spočítejte průřez trubice S2. (3 body)
V řešení použijte hustotu vody r = 1000 kg/m3.
[v2 = 15 m/s; S2 = 10 cm2]
|
|
27
|
Kovová tyč o průřezu S = 1 cm2 se pod vlivem síly prodlouží o Dl = 0,1 mm. Její klidová délka je l0 = 80 cm. Youngův modul pružnosti je E = 2.109 Pa.
a) Jaké je relativní prodloužení e? (2 body)
b) Spočítejte napětí s. (2 body)
c) Spočítejte sílu F působící na tyč. (2 body)
d) Jaké bude prodloužení tyče, bude-li na ní působit trojnásobná síla?. (2 body)
|
Datum poslední aktualizace:
27.6.2000 16:17:19