| Poř. |
Zadání |
|
1
|
Uvažujme směs
ideálních plynů tvořenou molekulárním kyslíkem O2 a vodíkem H2. Zjistěte, jak se změní tlak, molární tepelné kapacity CV, Cp, celkové tepelné kapacity nCV, nCp a Poissonova konstanta κ, necháme-li oba plyny zreagovat na vodní páru a tu přivedeme
za konstantního objemu opět na původní teplotu. Předpokládejte, že složky jsou
ve směsi v takovém poměru, že obě zcela zreagují.
Změna tlaku ... 2 body, Tepelné kapacity ... 1 + 1 + 1 + 1 bod,
Poissonova konstanta ...2 body
[změna látkového množství: n2/n1 = 2/3; tlak: p2/p1 = n2/n1 = 2/3; molární tepelné kapacity: CV2/CV1 = 6/5, Cp2/Cp1 = 8/7, celkové tepelné kapacity: n2CV2/n1CV1 = 4/5; n2Cp2/n1Cp1 = 16/21; Poissonova konstanta: κ2/κ1 = 20/21, přesto, že molární tepelné kapacity se zvýší vlivem zvýšení počtu stupňů volnosti, celkové tepelné kapacity naopak poklesnou vlivem snížení látkového množství]
Maximum 8 bodů, průměr 4,58 bodů (57,2%), s = 2,63, 19 testů.
|
|
2
|
Jeden mol
ideálního plynu s hodnotou poissonovy konstanty κ = 1,25 necháme expandovat
na dvojnásobný objem.
a) Jaká bude hodnota molární tepelné kapacity CV? (2 body)
Jaké teplo musíme dodat, má-li expanze probíhat
b) izotermicky (2 body)
c) izobaricky (2 body)
d) adiabaticky? (2 body)
[a) CV = 4R (počet stupňů volnosti i=8); b) Q = nRTln2; c) Q = 5pV; d) Q = 0 (z definice adiabatického děje)]
Maximum 8 bodů, průměr 5,89 bodů (73,6%), s = 2,08, 18 testů.
|
|
3
|
Vzduch
(předpokládejte, že je složen z dvouatomových molekul) izobaricky expanduje z
objemu V1 = 1 m³ na objem V2 = 2 m³ při tlaku p
= 105 Pa. Výchozí teplota je T1 = 400 K.
a) Jak se změní entropie? (5 bodů)
b) Jaká je hodnota molární tepelné kapacity za konstantního tlaku Cp?
(3 body)
[a) ΔS = nCpln(V2/V1) = 5/2 p0V0/T0.ln2; b) Cp = 7/2 R]
Maximum 8 bodů, průměr 5,67 bodů (70,8%), s = 2,35, 12 testů.
|
|
4
|
Ideální jednoatomový plyn ohřejeme dodáním tepla Q = 1 J.
Výchozí tlak, teplota a objem je p0, T0 a V0.
Jak se změní teplota
a) Při konstantním tlaku? (4 body)
b) Při konstantním objemu? (4 body)
[a) ΔT = 2T0/5p0T0; b) ΔT = 2T0/3p0T0]
Maximum 8 bodů, průměr 7,00 bodů (87,5%), s = 2,22, 14 testů.
|
|
5
|
Ideální jednoatomový plyn adiabaticky stlačíme na 1/4 původního objemu. Zadána je výchozí teplota T, tlak p a objem V.
a) Jak se změní tlak? (2 body)
b) Jaké teplo se odebere? (2 body)
c) Jak se změní vnitřní energie plynu? (2 body)
d) Jakou mechanickou práci je na stlačení třeba vykonat? (2 body)
[a) p2/p1 = (V2/V1)κ;
b) Q = 0 (z definice adiabatického děje);
c) ΔU = nCV(T2 - T1) = nCV(p2V2 - p1V1) = 3/2.nRpV(4κ-1 - 1) = 3/2.(pV)²/T.(4κ-1 - 1) ;
d) A = ΔU]
Maximum 8 bodů, průměr 5,83 bodů (72,9%), s = 1,33, 6 testů.
|
|
6
|
Mějme stojaté vlnění, jehož výchylka jako funkce času je
dána jako u(x, t) = 12 cos(πx).sin(4πt) kde čas je v sekundách,
souřadnice x v metrech a výchylka u(x, t) v milimetrech.
a) Jakou amplitudu budou mít kmity měřené v bodě x = 1/2 m? (2 body)
b) Jaká bude rychlost kmitání ve stejném bodě
x = 1/2 m? (2 body)
c) Jaká je amplituda postupných vln, ze kterých zadané stojaté vlnění vzniklo?
(1 bod)
d) Jaká je perioda kmitů? (1 bod)
e) Najděte souřadnice uzlů. (1 bod)
f) Najděte souřadnice kmiten. (1 bod
[a) 0 mm; b) 0 m/s; c) U0 = 6 mm; d) T = 0,5 s e) xuzly = (2n + 1)/2 m, kde n je celé číslo; f) xkmitny = n m, kde n je celé číslo]
Maximum 8 bodů, průměr 7,00 bodů (87,5%), s = 1,41, 10 testů.
|
|
7
|
Fyzikální kyvadlo má tvar polokoule zavěšené ve středu,
moment setrvačnosti je stejný jako moment setrvačnosti koule, J = 2/5 mR2 kde m je hmotnost polokoule, R je poloměr (viz obrázek na tabuli). Vzdálenost těžiště od středu je RT = 3/8 R.
a) Spočítejte úhlovou frekvenci malých kmitů. (3 body)
b) Spočítejte redukovanou délku kyvadla. (2 body)
c) Jaká bude úhlová frekvence, zavěsíme-li kruhovou výseč ve vrcholu (tj. v bodě ve vzdálenosti R od středu na ose symetrie)? (3 body)
Gravitační zrychlení uvažujte g = 10 ms-2
[ω2 = 15g/16R; b) l = 16/15 R; c) ω2 = 25g/26R]
Maximum 8 bodů, průměr 8,00 bodů (100,0%), s = 2,16, 10 testů.
|
|
8
|
Lineární harmonický oscilátor kmitá s úhlovou frekvencí
4π s-1. Hmotnost kmitajícího systému je m = 2 kg. Amplituda je
U0 = 0,2 m.
a) Spočítejte energii oscilátoru. (2 body)
b) Jaká je tuhost systému? (2 body)
c) Napište pohybovou rovnici tohoto oscilátoru, jak obecně tak číselně. (2 body)
d) Napište nějaké netriviální řešení této rovnice. (2 body)
[E = ½ mω2U02 = 6,4 J; b) k = ω2/m = 320 N/m; c) d2x/dt2 + ω2x = 0; d2x/dt2
+ 16π2x = 0; d) např. cos(4πt)]
Maximum 8 bodů, průměr 6,00 bodů (75,0%), s = 1,93, 8 testů.
|
|
9
|
Tlumený lineární harmonický oscilátor s frekvencí f = 50 Hz
má v čase t0 = 0 s amplitudu U0 = 20 cm, v čase t1
= 5 s amplitudu U1 = 15 cm.
a) Jaká je konstanta tlumení δ? (2 body)
b) Jaký je logaritmický dekrement útlumu Λ? (2 body)
c) Jaký je poměr energií v časech t0 a t1? (2 body)
d) Jaká bude amplituda v čase t2 = 10 s? (2 body)
[a) δ = 1/5 ln(4/3); b) Λ = δ/f
= 0,00115; c) E0/E1 = (U0/U1)2
= 16/9; d) U(10 s) = (3/4)2U0 = 11,25 cm]
Maximum 8 bodů, průměr 6,60 bodů (82,5%), s = 2,37, 10 testů.
|
|
10
|
Mějme stojaté vlnění, jehož výchylka jako funkce času je
dána jako u(x, t) = 6 cos(πx/2).sin(4πt) kde čas je v sekundách,
souřadnice x v metrech a výchylka u(x, t) v milimetrech.
a) Jakou amplitudu budou mít kmity měřené v bodě x = 1/2 m? (3 body)
b) Jaká je fázová rychlost, amplituda a vlnová délka postupných vln, ze kterých zadané stojaté vlnění vzniklo? (3 body)
c) Jaká je perioda kmitů? (1 bod)
d) Najděte souřadnice kmiten. (1 bod)
[[a) U(x = 1/2 m) = 6/1,414 = 4,24 mm; b) vf
= ω/k = 8 m/s; U0 = 3 mm; λ = 2π/k = 4 m; c) T = 0,5 s;
d) xkmitny = 2n, kde n je celé číslo]
Maximum 8 bodů, průměr 7,20 bodů (90,0%), s = 0,45, 5 testů.
|
|
11
|
Fyzikální kyvadlo má tvar hmotné tyče délky 1 m zavěšené na jednom konci, na
druhém konci je pevně připevněno závaží. Hmotnosti tyče i závaží jsou shodná, 2
kg. Moment setrvačnosti tyče vzhledem ke kolmé ose procházející středem je
1/12 ml2 kde l je délka tyče. Průřez tyče a rozměry závaží zanedbejte.
a) Jaký je moment setrvačnosti kyvadla? (3 body)
b) Spočítejte úhlovou frekvenci malých kmitů kyvadla. (3 body)
c) Spočítejte redukovanou délku kyvadla. (2 body)
Gravitační zrychlení uvažujte g = 10 ms-2.
[a) J = 4/3 ml2 = 8/3 kgm2;
b) ω2 = 9g/8R;
c) l = 8/9 R]
Maximum 8 bodů, průměr 2,20 bodů (27,5%), s = 2,49, 5 testů.
|
|
12
|
Lineární harmonický oscilátor kmitá s úhlovou frekvencí 4π s-1.
Tuhost systému je 2 N/m.
a) Spočítejte hmotnost kmitající části oscilátoru. (2 body)
b) Jaká je amplituda oscilátoru, je-li jeho energie rovna 4 J? (2 body)
c) Napište pohybovou rovnici tohoto oscilátoru, jak obecně tak číselně. (2 body)
d) Napište nějaké netriviální řešení této rovnice. (2 body)
[m = k/ω2 = 2/16π2 = 1/80 kg; b) U2 = E/ω2m = 2E/k = 4 m2; U = 2 m; c) d2x/dt2 + ω2x = 0; d2x/dt2
+ 16π2x = 0; d) např. cos(4πt)]
Maximum 8 bodů, průměr 7,00 bodů (87,5%), s = 1,26, 6 testů.
|
|
13
|
Tlumený lineární harmonický oscilátor s frekvencí f =
10 Hz má logaritmický dekrement útlumu Λ = 0,01. V čase t0 = 0
má amplitudu U0 = 20 cm,
a) Jaká je konstanta tlumení δ? (2 body)
b) Jaká bude amplituda v čase t1 = 10 s? (2 body)
c) Jaký je poměr energií v časech t0 a t1?
(2 body)
d) Za jak dlouho klesne hodnota energie oscilátoru na jednu čtvrtinu? (2 body)
[a) δ = Λf = 0,1 s-1;
b) U(t = 10 s) = 20/e = 7,36 cm;
c) E0/E1 = (U0/U1)2
= e2 = 7,39; d) E0/E2
= (U0/U2)2 = e2δt = 4, t = 1/2δ
ln4 = 1/δ ln2 = 6,9 s]
Maximum 8 bodů, průměr 6,00 bodů (75,0%), s = 2,00, 5 testů.
|
|
14
|
a) Spočítejte, relativní změnu
frekvence akustického zdroje o frekvenci 1 kHz, umístěného na automobilu,
zaregistruje pozorovatel, míjí-li ho automobil rychlostí 118,8 km/h? Rychlost
zvuku předpokládejte c = 330 m/s. (3 body)
b) Jaká bude relativní změna frekvence, bude-li pozorovatel v automobilu a akustický zdroj v klidu mimo automobil?
Bude větší nebo menší? (3 body)
c) Záleží relativní změna frekvence i na frekvenci zdroje? (2 body)
Maximum 8 bodů, průměr 7,75 bodů (96,9%), s = 0,46, 8 testů.
|
|
15
|
Spočítejte intenzitu
elektrického pole E elektromagnetického záření vyzařovaného ze slunce v
blízkosti slunečního povrchu, je-li celkový vyzařovaný výkon slunce P = 3,827.1026
W. (4 body)
Jaká bude intenzita záření I v
místě země, je-li poloměr slunce R = 6,96.105 km a poloměr oběžné
dráhy země r = 1,5.108 km? (4 body)
Maximum 8 bodů, průměr 7,14 bodů (89,3%), s = 0,38, 7 testů.
|
|
16
|
Jaká je hodnota mřížkové
konstanty, dochází-li k interferenci čtvrtého řádu ve směru 30° od přímého
směru? Vlnová délka světla je λ = 800 nm. (4 body)
Jaky nejvyšší řád interference může u teto mřížky při teto
vlnové délce vzniknout? (4 body)
[a) d = 6,4.10-6 m; b) kmax = 7(pozn.: Řád interference 8 odpovídá úhlu 90 stupňů, to již nelze pozorovat na stínítku)]
Maximum 8 bodů, průměr 7,78 bodů (97,2%), s = 0,67, 9 testů.
|
|
17
|
Poloha předmětu je a = -40 cm,
poloha obrazu získaného zobrazením zrcadlem je -10 cm.
a) Jaká je ohnisková vzdálenost zrcadla f? (2 body)
b) Jaký je jeho poloměr r? (2 body)
c) Jedná se o duté nebo o vypuklé zrcadlo? (1 bod)
d) Jaké je zvětšení z? (1 bod)
e) Je obraz vzpřímený nebo převrácený? (1 bod)
f) Nakreslete obrázek s vyznačením alespoň dvou význačných paprsků. (1 bod)
[a) f = -8 cm b) r = -16cm; c) duté; d) z = -0,25; e) převrácený]
Maximum 8 bodů, průměr 7,90 bodů (98,8%), s = 0,32, 10 testů.
|
|
18
|
Při ozvučování sálu bylo zjištěno, že dvěma
reproduktorovými soustavami dosáhneme v nějakém místě sálu hladinu akustického
tlaku zkušebního signálu Lp = 60
dB.
a) Jaké hladiny akustického tlaku dosáhneme, použijeme-li pro ozvučení 4 stejné reproduktorové soustavy? (2 body)
b) Kolikrát se zvýší akustický tlak? (2 body)
c) Kolikrát se zvýší intenzita zvuku? (2 body)
d) Jak se změní hladina intenzity? (2 body)
[a) Lp = 63 dB; b) p2/p1 =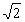 ; c) I2/I1 = 2; d) ΔLI = ΔLp = 3 dB] ; c) I2/I1 = 2; d) ΔLI = ΔLp = 3 dB]
Maximum 8 bodů, průměr 3,88 bodů (48,4%), s = 2,64, 8 testů.
|