| Poř. |
Zadání |
|
1
|
Jsou zadány polynomy
P(x) = x6 + 2x5 + x4 + 2x3 + x,
Q(x) = x2 + 1.
Najděte podíl Y(x) a zbytek Z(x).
[Y(x) = x4 + 2x3, Z(x) = x]
Maximum 4 body, průměr 3,86 bodů (96,6%), s = 0,47, 22 testů.
|
|
2
|
Jsou zadány polynomy
P(x) = x6 + 2x5 + x4 − 2x3 + x,
Q(x) = x2 + 1.
Najděte podíl Y(x) a zbytek Z(x).
[Y(x) = x4 + 2x3 − 4x, Z(x) = 5x]
Maximum 4 body, průměr 3,41 bodů (85,3%), s = 1,09, 29 testů.
|
|
3
|
Je zadán polynom
P(x) = 2x5 − 11x4 + 20x3 − 16x2 + 16x − 16.
a) Rozložte na součin ireducibilních polynomů.
b) Zjistěte násobnost kořene 2.
Návod: začněte řešením b).
[(x − 2)3(2x2 + x + 2), násobnost kořene 2 je 3]
Maximum 4 body, průměr 2,52 bodů (62,9%), s = 1,56, 58 testů.
|
|
4
|
Je zadán polynom
P(x) = 2x6 + x5 + 2x4 − 2x2 − x − 2.
a) Najděte reálné kořeny, víte-li, že jeden kořen je j.
b) Napište P(x) jako součin ireducibilních polynomů.
[Reálné kořeny jsou +1 a −1; P(x) = (x2+1)(x − 1)(x + 1)(2x2 + x + 2)]
Maximum 4 body, průměr 2,61 bodů (65,3%), s = 1,38, 18 testů.
|
|
5
|
Je zadán polynom
P(x) = 2x6 + x5 + 2x4 − 2x2 − x − 2.
Napište P(x) jako součin ireducibilních polynomů.
[P(x) = (x2+1)(x − 1)(x + 1)(2x2 + x + 1)]
Maximum 4 body, průměr 3,50 bodů (87,5%), s = 0,82, 16 testů.
|
|
6
|
Rozložte polynom x4 − 2x3 − 2x2 + 8x − 8 na součin ireducibilních polynomů, znáte-li dva kořeny x1 = 2 a x2 = 1 + j. (4 body).
[(x − 2)(x + 2)(x2 − 2x + 2)]
Maximum 4 body, průměr 2,58 bodů (64,5%), s = 1,46, 19 testů.
|
|
7
|
Mějme maticovou rovnici XA − A = E kde A = ((3, 2, 1),(2, 1, 1), (1, 1, −1)) a E je jednotková matice (typu (3, 3)). Vypočtěte X.
[Po úpravách dostaneme X = A−1 + E a vyjde X = ((3, −3, 1), (−3, 6, −1), (−1, 2, 0))]
Maximum 4 body, průměr 2,91 bodů (72,8%), s = 1,20, 45 testů.
|
|
8
|
1. Vypočtěte determinant matice A, jejíž řádky jsou (1, 1, 1, 1), (1, 2, 2, 2), (1, 3, 4, 4) a (1, 4, 7, 8). (2 body)
2. Vypočtěte inverzní matici k matici A, jejíž řádky jsou (2, 1) a (0, 1) (2 body).
[1. det A = 1; 2. A−1 = ((1/2, −1/2), (0, 1))]
Maximum 4 body, průměr 3,20 bodů (80,0%), s = 1,52, 15 testů.
|
|
9
|
Najděte souřadnice polynomu P(x) = 2x2 + 5x − 7 v uspořádané bázi {(x + 2)2, x + 2, 1}.
[(2, −3, −9)]
Maximum 4 body, průměr 3,64 bodů (91,1%), s = 1,06, 42 testů.
|
|
10
|
Spočítejte inverzní matici k matici A = ((3, 1, 2), (2, 3, 1), (4, 0, 3)).
[A = ((9, −3, −5), (−2, 1, 1), (−12, 4, 7))]
Maximum 4 body, průměr 2,67 bodů (66,7%), s = 1,51, 33 testů.
|
|
11
|
Spočítejte inverzní matici k matici A = ((0, 1, 2), (1, 2, 3), (2, 3, 3)).
[A = ((−3, 3, −1), (3, −4, 2), (−1, 2, −1))]
Maximum 4 body, průměr 2,81 bodů (70,3%), s = 1,47, 16 testů.
|
|
12
|
Polynom P(x) má souřadnice (−2, 1, 2) v bázi {x2 + 1, x2 + x, x + 1}.
a) Vypočítejte polynom P(x).
b) Najděte souřadnice polynomu v uspořádané bázi {2x2 + 2, x2 + 2x, 1}.
[a) P(x) = x2 + 3x; b) (−1/4, 3/2, 1/2)]
Maximum 4 body, průměr 2,40 bodů (60,1%), s = 1,29, 42 testů.
|
|
13
|
Nechť B = 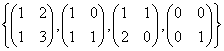 je uspořádaná báze nějakého lineárního podprostoru. je uspořádaná báze nějakého lineárního podprostoru.
a) Najděte souřadnice jednotkové matice typu (2, 2) v bázi B.
b) Určete dimenzi <B>.
[a) (1/2, 3/2, −1, −3); b) dim<B> = 4]
Maximum 4 body, průměr 2,21 bodů (55,3%), s = 1,69, 33 testů.
|
|
14
|
1. Vypočtěte determinant matice, jejíž řádky jsou (1, 1, 1, 1), (1, 2, 2, 2), (1, 3, 4, 4) a (1, 4, 7, 8). (2 body)
[detA = 2]
Maximum 4 body, průměr 3,83 bodů (95,7%), s = 0,57, 35 testů.
|
|
15
|
Jsou zadány polynomy P(x) = 3x2 + x + 4 a Q(x) = x2 − x. Polynom P(x) nechť má v bázi B = {b1, b2} souřadnice (3, 1), polznom Q(x) nechť má v téže bázi souřadnice (1, −1). Najděte bázi B.
[B = {x2 + 1, x + 1}]
Maximum 4 body, průměr 3,25 bodů (81,3%), s = 1,36, 24 testů.
|
|
16
|
Velká písemka, pondělní cvičení, varianta A.
Maximum 20 bodů, průměr 6,33 bodů (31,7%), s = 3,08, 9 testů.
|
|
17
|
Velká písemka, pondělní cvičení, varianta B.
Maximum 20 bodů, průměr 4,89 bodů (24,4%), s = 3,86, 9 testů.
|
|
18
|
Velká písemka, pondělní cvičení, varianta C.
Maximum 20 bodů, průměr 6,89 bodů (34,4%), s = 2,76, 9 testů.
|
|
19
|
Velká písemka, pondělní cvičení, varianta D.
Maximum 20 bodů, průměr 5,91 bodů (29,5%), s = 3,94, 11 testů.
|
|
20
|
Velká písemka, středeční cvičení, varianta E.
Maximum 20 bodů, průměr 6,70 bodů (33,5%), s = 3,71, 10 testů.
|
|
21
|
Velká písemka, středeční cvičení, varianta F.
Maximum 20 bodů, průměr 7,57 bodů (37,9%), s = 5,83, 7 testů.
|
|
22
|
Velká písemka, středeční cvičení, varianta G.
Maximum 20 bodů, průměr 6,43 bodů (32,1%), s = 4,54, 7 testů.
|
|
23
|
Velká písemka, středeční cvičení, varianta H.
Maximum 20 bodů, průměr 7,11 bodů (35,6%), s = 5,23, 9 testů.
|
|
24
|
Velká písemka, čtvrteční cvičení, varianta A.
Maximum 20 bodů, průměr 11,61 bodů (58,0%), s = 6,87, 23 testů.
|
|
25
|
Velká písemka, čtvrteční cvičení, varianta B.
Maximum 20 bodů, průměr 9,06 bodů (45,3%), s = 5,40, 17 testů.
|
|
26
|
Velká písemka, páteční cvičení, varianta A.
Maximum 20 bodů, průměr 11,95 bodů (59,8%), s = 6,05, 21 testů.
|
|
27
|
Velká písemka, páteční cvičení, varianta B.
Maximum 20 bodů, průměr 11,64 bodů (58,2%), s = 4,78, 14 testů.
|