| Poř. |
Zadání |
|
1
|
Je zadán polynom
P(x) = x5 +; 8x4 + 7x3 − 52x2 − 44x + 80.
a) Je 1 kořen?.
b) Zjistěte násobnost kořene 1.
c) Najděte všechny kořeny.
d) Vyjádřete P(x) jako součin kořenových činitelů.
[Ano; 1; 1, 2, −2, −4, −5; (x − 1)(x − 2)(x + 2)(x + 4)(x + 5)]
Maximum 4 body, průměr 2,63 bodů (65,7%), s = 1,00, 67 testů.
|
|
2
|
Je zadán polynom
P(x) = x5 + 5x4 − 24x3 − 120x2 − 25x − 125.
Vyjádřete P(x) jako součin ireducibilních polynomů, víte-li, že jeden kořen je j.
Nápověda: polynom má všechny reálné kořeny celočíselné.
[(x2 + 1)(x + 5)2(x − 5)]
Maximum 4 body, průměr 2,69 bodů (67,2%), s = 1,45, 32 testů.
|
|
3
|
Je zadán polynom
P(x) = 2x5 − 11x4 + 20x3 − 16x2 + 16x − 16.
a) Zjistěte násobnost kořene 2.
b) Vyjádřete P(x) jako součin ireducibilních polynomů.
[3; (2x2 + x + 2)(x − 2)3]
Maximum 4 body, průměr 3,64 bodů (91,0%), s = 0,76, 53 testů.
|
|
4
|
Jsou zadány polynomy
P(x) = x4 − 18x2 + 81 a Q(x) = x2 − 2.
a) Najděte zbytek podílu P(x)/Q(x). Jaký má zbytek stupeň? (2 body).
b) Zjistěte násobnost kořene 3 (2 body).
[49, stupeň zbytku je 0, podle věty o dělení polynomů <= 1, obě odpovědi jsou akceptovány; kořen 3 je dvojnásobný]
Maximum 4 body, průměr 3,25 bodů (81,3%), s = 0,71, 40 testů.
|
|
5
|
Polynom P(x) má souřadnice (−2, 1, 2) v bázi {x2 + 1, x2 + x, x + 1}.
a) Vypočítejte polynom P(x).
b) Najděte souřadnice polynomu v uspořádané bázi {2x2 + 2, x2 + 2x, 1}.
[a) P(x) = −x2 + 3x; b) (−5/4, 3/2, 5/2)]
Maximum 4 body, průměr 1,67 bodů (41,7%), s = 1,46, 18 testů.
|
|
6
|
Je zadána množina M = <{3x3 + 1, x2 + x, 2x + 2, 3x2 − 1, 2x2 − 2}>.
a) Je množina M lineární podprostor? (1 bod)
b) Jaká je dimenze množiny M? (1 bod)
c) Najděte nějakou bázi množiny M (2 body).
[a) Ano, lineární obal je vždy lineárním podprostorem; dimM = 4; například {3x3 + 1, x2 + x, x + 1; 1}]
Maximum 4 body, průměr 3,41 bodů (85,3%), s = 1,02, 29 testů.
|
|
7
|
Je zadána množina M = <{3x3 + 1, x2 + x, 2x + 2, 3x2 − x, 2x2 − 2}>.
a) Je množina M lineární podprostor? (1 bod)
b) Jaká je dimenze množiny M? (1 bod)
c) Najděte nějakou bázi množiny M (2 body).
[a) Ano, lineární obal je vždy lineárním podprostorem; dimM = 3; například {3x3 + 1, x2 + x, 2x + 2} což jsou první tři ze zadaných vektorů]
Maximum 4 body, průměr 3,33 bodů (83,3%), s = 0,82, 15 testů.
|
|
8
|
1. Vypočtěte determinant matice A, jejíž řádky jsou (2, 2, 2, 2), (1, 2, 2, 2), (1, 3, 4, 4) a (1, 1, 7, 8). (4 body)
[2]
Maximum 4 body, průměr 3,23 bodů (80,7%), s = 1,07, 22 testů.
|
|
9
|
Najděte řešení X maticové rovnice AX + EX + 0X + X = B, kde 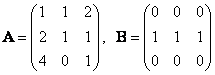 . .
[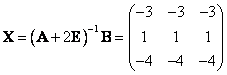 ] ]
Maximum 4 body, průměr 0,77 bodů (19,2%), s = 1,17, 13 testů.
|
|
10
|
Najděte řešení X maticové rovnice AX + EX + 0X + X = B, kde A =  , B = , B = 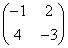 . .
[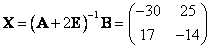 ] ]
Maximum 4 body, průměr 1,67 bodů (41,7%), s = 1,68, 21 testů.
|
|
11
|
Najděte řešení X maticové rovnice AX + EX + B = 0X + X + C, kde A = 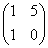 , B = , B = 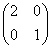 a C = a C = 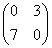 . .
[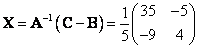 ] ]
Maximum 4 body, průměr 3,37 bodů (84,3%), s = 0,88, 27 testů.
|
|
12
|
zápočtová písemka, pátek 9:15, varianta I
Maximum 20 bodů, průměr 9,55 bodů (47,7%), s = 3,83, 11 testů.
|
|
13
|
zápočtová písemka, pátek 9:15, varianta J
Maximum 20 bodů, průměr 9,91 bodů (49,5%), s = 5,68, 11 testů.
|
|
14
|
zápočtová písemka, pátek 11:00 varianta K
Maximum 20 bodů, průměr 11,63 bodů (58,1%), s = 4,37, 8 testů.
|
|
15
|
zápočtová písemka, pátek 11:00, varianta L
Maximum 20 bodů, průměr 10,20 bodů (51,0%), s = 3,68, 10 testů.
|
|
16
|
Zápočtová písemka, pondělní cvičení, varianta M.
Maximum 20 bodů, průměr 12,00 bodů (60,0%), s = 5,92, 9 testů.
|
|
17
|
Zápočtová písemka, pondělní cvičení, varianta N.
Maximum 20 bodů, průměr 11,90 bodů (59,5%), s = 4,28, 10 testů.
|
|
18
|
Zápočtová písemka, úterní cvičení, varianta O.
Maximum 20 bodů, průměr 8,47 bodů (42,4%), s = 4,56, 19 testů.
|
|
19
|
Zápočtová písemka, úterní cvičení, varianta P.
Maximum 20 bodů, průměr 9,37 bodů (46,8%), s = 4,14, 19 testů.
|
|
20
|
Zápočtová písemka, středeční a čtvrteční cvičení, varianta Q.
Maximum 20 bodů, průměr 12,89 bodů (64,4%), s = 4,62, 36 testů.
|
|
21
|
Zápočtová písemka, středeční a čtvrteční cvičení, varianta R.
Maximum 20 bodů, průměr 10,54 bodů (52,7%), s = 4,08, 35 testů.
|