| Poř. |
Zadání |
|
1
|
Je zadána matice  . .
a) Spočítejte AT.
b) Spočítejte A2.
c) Spočítejte detA.
d) Spočítejte A−1.
[a) AT = A neboť jde o symetrickou matici; b) 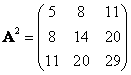 ; c) detA = 0; d) inverzní matice neexistuje] ; c) detA = 0; d) inverzní matice neexistuje]
Maximum 4 body, průměr 3,47 bodů (86,7%), s = 0,74, 49 testů.
|
|
2
|
Je zadána matice  . .
a) Spočítejte AT.
b) Spočítejte A2.
c) Spočítejte detA.
d) Spočítejte A−1.
[a) AT = A neboť jde o symetrickou matici; b) 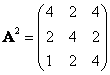 ; c) detA = 0; d) ; c) detA = 0; d) 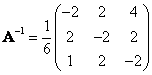 ] ]
Maximum 4 body, průměr 3,35 bodů (83,8%), s = 0,70, 17 testů.
|
|
3
|
Je zadána matice  . .
a) Spočítejte AT.
b) Spočítejte A2.
c) Spočítejte detA.
d) Spočítejte A−1.
[a) 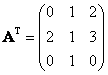 ; b) ; b) 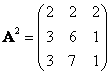 ; c) detA = 4; d) ; c) detA = 4; d) 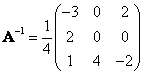 ] ]
Maximum 4 body, průměr 2,76 bodů (69,1%), s = 1,05, 34 testů.
|
|
4
|
Jsou zadány tři vektory a = (1, 1, −1), b = (2, 1, 1) a c = (1, 2, 0).
a) Jsou vektory a, b a c bází?
b) Vyjádřete vektor x = (2, −1, −1) jako lineární koémbinaci vektorů a, b a c.
c) Patří vektor x do lineárního obalu vektorů a, b a c?.
d) Najděte souřadnice vektoru x v uspořádané bázi {c, b, a}.
[a) vektory jsou lineárně nezávislé, proto jsou bází (nějakého podprostoru); b) x = 2a + b − 2c; c) patří, neboť vektor x lze vyjádřit (podle řešení bodu b) ) jako lineární kombinaci generátorů a, b a c; d) souřadnice jsou −2, 1 a 2]
Maximum 4 body, průměr 2,50 bodů (62,5%), s = 1,15, 46 testů.
|
|
5
|
Jsou zadány lineární podprostory
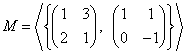 , , 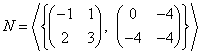 . .
a] Určete dimenze lineárních podprostorů M a N.
b) Jsou množiny M a N tytéž podprostory?
c) Určete dimenzi průniku M∩N.
d) Určete dimenzi spojení MvN.
e) Bonusová otázka: nakreslete množinový diagram, vyznačte v něm množiny M, N, M∩N a MvN.
[a) dimM = 2, dimN = 2; b) Množiny M a N jsou jeden a týž lineární podprostor; c) dimM∩N = 2; d) dimMvN = 2]
Maximum 4 body, průměr 2,60 bodů (65,0%), s = 1,29, 25 testů.
|
|
6
|
Jsou zadány lineární podprostory
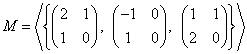 , , 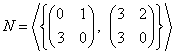 . .
a) Určete dimenze lineárního podprostoru M.
b) Určete dimenze lineárního podprostoru N.
c) Jsou množiny M a N tytéž podprostory?
d) Určete dimenzi průniku M∩N.
e) Bonusová otázka: nakreslete množinový diagram, vyznačte v něm množiny M, N, M∩N a MvN.
[a) dimM = 2; b) dimN = 2; c) Množiny M a N jsou jeden a týž lineární podprostor; d) dimM∩N = 2]
Maximum 4 body, průměr 1,41 bodů (35,3%), s = 1,23, 17 testů.
|
|
7
|
Zápočtová písemka, varianta A.
Příklad na lineární prostor: Nechť L je lineární prostor polynomů stupně nejvýše 3 a B = {(1, x + 1, (x + 1)2, (x + 1)3)} je jeho uspořádaná báze. Najděte souřadnice polynomu P(x) = 2x3 − x2 + 2x + 1 v této bázi.
[−4, 10, −7, 2]
Maximum 20 bodů, průměr 7,43 bodů (37,1%), s = 5,53, 7 testů.
|
|
8
|
Zápočtová písemka, varianta B.
Příklad na lineární prostor: Pro která reálná čísla t je vektor (7, −2, t) lineární kombinací vektorů (2, 3, 5), (3, 7, 8) a (1, −6, 1)?
[t = −15]
Maximum 20 bodů, průměr 6,63 bodů (33,1%), s = 3,85, 8 testů.
|
|
9
|
Zápočtová písemka, varianta C.
Příklad na lineární prostor: Pro která reálná čísla t patří vektor (−3, 2, t) do lineárního obalu vektorů (2, 3, −5),
(−1, 1, –5) a (2, 1, 1)?
[pro t = −12]
Maximum 20 bodů, průměr 9,00 bodů (45,0%), s = 4,00, 16 testů.
|
|
10
|
Zápočtová písemka, varianta D.
Maximum 20 bodů, průměr 6,69 bodů (33,4%), s = 3,38, 16 testů.
|
|
11
|
Zápočtová písemka, varianta E.
Příklad na lineární prostor: Pro která reálná čísla t je vektor (3, 1, t) lineární kombinací vektorů (−2, −3, 5), (1, 2, −4) a (−2, −1, −1)?
[pro t = 3]
Maximum 20 bodů, průměr 12,90 bodů (64,5%), s = 3,81, 10 testů.
|
|
12
|
Zápočtová písemka, varianta F.
Příklad na lineární prostor: Pro která reálná čísla t je množina 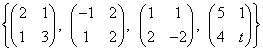 bází? bází?
[pro t ≠ 3]
Maximum 20 bodů, průměr 9,25 bodů (46,3%), s = 6,02, 8 testů.
|
|
13
|
Zápočtová písemka, varianta G.
Příklad na lineární prostor: Vektor x má v uspořádané bázi B = {b1, b2, b3} souřadnice (2, 1, −1). Jaké má tentýž vektor souřadnic v bázi C = {2b1 + 3b2 − 3b3, b1 + 2b2 − b3,− b1 − b3}? Odůvodněte, že C je skutečně báze.
[(1, −1, −1), C je báze, neboť řešení vyjde jednoznačně, lze také odůvodnit tak, že řešení přidružené homogenní soustvy vyjde triviální (matice soustavy je regulární, po GEM vyjde troujúhelniková matice) a vektorový vztah lineární kombinace vektorů položena rovna nulovému vektoru vede na tutéž soustavu, tedy vektory jsou lineárně nezávislé]
Maximum 20 bodů, průměr 8,00 bodů (40,0%), s = 3,35, 6 testů.
|
|
14
|
Zápočtová písemka, varianta H.
Příklad na lineární prostor: Napište vektor (7, 7, 7) jako lineární kombinaci vektorů a = (2, 3, 5), b = (−1, −2, −4) a c = (2, 1, −1). Jsou vektory a, b a c bází? Odůvodněte.
[řešení je nekonečně mnoho, například (7, 7, 7) = a − b + 2c, koeficienty lineární kombinace lze obecně vyjádřit jako (α β, &gama;) = (1, −1, 2) + t(3, 4, −1), což však v zadání nebylo požadováno, na plný počet bodů stačilo jen jedno z řešení; vektory a, b a c nejsou bází, jsou lineárně závislé, což je zřejmé z matice řešené soustavy, kde se při Gaussově eliminaci vynuloval jeden řádek, řeší-li se soustava rovnic pro ověření lineární nezávislosti vektorů a, b a c, dostaneme tutéž matici soustavy, odlišnost je pouze v pravé straně, která bude nulová, GEM se však bude provádět shodně]
Maximum 20 bodů, průměr 11,14 bodů (55,7%), s = 2,48, 7 testů.
|
|
15
|
Zápočtová písemka, varianta I.
Příklad na lineární prostor: Najděte nějakou bázi a určete dimenzi lineárního podprostoru M = <{(0, −2, −3, 2), (−2, 5, 2, −3), (−2, 1, −4, 1), (−4, 4, −5, 0)}>.
[například {(0, −2, −3, 2), (−2, 5, 2, −3)}, dimM = 2]
Maximum 20 bodů, průměr 9,50 bodů (47,5%), s = 4,31, 8 testů.
|
|
16
|
Zápočtová písemka, varianta J.
Příklad na lineární prostor: Vektor x má v uspořádané bázi B = {(2, 3, 1), (−3, 3, 1), (2, −2, −3)} souřadnice 2, 1 a –1. Jaké má tentýž vektor souřadnice v uspořádané bázi C = {(1, 1, 1), (−1, 0, 1), (0, 2, 1)}?
[1, 2, 3]
Maximum 20 bodů, průměr 11,57 bodů (57,9%), s = 4,28, 7 testů.
|