| Poř. |
Datum |
Zadání |
|
1
|
20.10.1999
středa 7,30'
doba:
11/2 minut
|
Ideální plyn změní objem z hodnoty V1 na hodnotu V2 při konstantní teplotě T.
a) Jakou práci systém vykoná? (2 body)
b) Jak se změní vnitřní energie plynu? (1 bod)
c) Jaké teplo se při tomto dějí musí plynu dodat? (1 bod)
[a) A = nRln(V2/V1); b) DU = 0 … jde o izotermický děj; c) Q = A]
Maximum 4 body, průměr 3,14 bodů (78,4%), s = 1,17, 22 testů.
|
|
2
|
20.10.1999
středa 7,30'
doba:
11/2 minut
|
Ideální plyn má hodnotu Poissonovy konstanty k = 1,1.
a) Kolik stupňů volnosti má jedna molekula? (1 bod)
b) Jaká je hodnota molární tepelné kapacity při konstantním objemu Cv? (1 bod)
c) Jaká je hodnota molární tepelné kapacity při konstantním tlaku Cp? (1 bod)
c) Jaká je vnitřní energie pro n molů tohoto plynu a pro teplotu T? (1 bod)
[a) i = 20; b) Cv = 10 R; b) Cp = 11 R; d) U = 10 nRT]
Maximum 4 body, průměr 3,59 bodů (89,8%), s = 0,73, 22 testů.
|
|
3
|
20.10.1999
středa 12,45'
doba:
15/2 minut
|
Ideální plyn má hodnotu Poissonovy konstanty k = 1,2.
Výchozí tlak, teplota a objem je p0, T0 a V0.
a) Jaké teplo musíme dodat, má-li plyn zvýšit teplotu o 10°C při konstantním objemu? (3 body)
b) Jaká je hodnota molární tepelné kapacity při konstantním tlaku Cp? (1 bod)
[a) Q = 50 p0V0/T0; b) Cp = 5 R]
Maximum 4 body, průměr 3,32 bodů (82,9%), s = 1,16, 19 testů.
|
|
4
|
20.10.1999
středa 12,45'
doba:
15/2 minut
|
Ideální jednoatomový plyn ohřejeme dodáním tepla Q = 1 J. Výchozí tlak, teplota a objem je p0, T0 a V0. Jak se změní teplota
a) Při konstantním tlaku? (2 body)
b) Při konstantním objemu? (2 body)
[a) DT = 2T0/5p0T0; b) DT = 2T0/3p0T0]
Maximum 4 body, průměr 2,70 bodů (67,5%), s = 1,38, 20 testů.
|
|
5
|
22.10.1999
pátek 11,00'
doba:
15/2 minut
|
Ideální plyn má hodnotu Poissonovy konstanty k = 1,1.
a) Kolik stupňů volnosti má jedna molekula? (1 bod)
b) Jaká je hodnota molární tepelné kapacity při konstantním objemu Cv? (1 bod)
c) Jaká je hodnota molární tepelné kapacity při konstantním tlaku Cp? (1 bod)
c) Jaká je vnitřní energie pro 1 mol tohoto plynu a pro teplotu T? (1 bod)
Hodnotu molární plynové konstanty uvažujte R = 8 J/K.mol.
[a) i = 20; b) Cv = 80 J/K.mol; b) Cp = 88 J/K.mol; d) U = 80T]
Maximum 4 body, průměr 3,72 bodů (93,1%), s = 0,75, 18 testů.
|
|
6
|
22.10.1999
pátek 11,00'
doba:
15/2 minut
|
Ideální plyn má hodnotu Poissonovy konstanty k = 1,2.
Výchozí tlak, teplota a objem je p1 = 105 Pa, T1 = 400 K a V1 = 1 m3.
a) Jaké teplo musíme dodat, má-li plyn zvýšit teplotu o 10°C při konstantním objemu? (4 body)
[Q = 50 p0V0/T0]
Maximum 4 body, průměr 3,41 bodů (85,3%), s = 0,62, 17 testů.
|
|
7
|
22.10.1999
pátek 7,30'
doba:
18/2 minut
|
Ideální plyn má hodnotu Poissonovy konstanty k = 1,1.
a) Kolik stupňů volnosti má jedna molekula? (1 bod)
b) Jaká je hodnota molární tepelné kapacity při konstantním objemu Cv? (1 bod)
c) Jaká je hodnota molární tepelné kapacity při konstantním tlaku Cp? (1 bod)
c) Jaká je vnitřní energie pro 1 mol tohoto plynu a pro teplotu T? (1 bod)
Hodnotu molární plynové konstanty uvažujte R = 8 J/K.mol.
[a) i = 20; b) Cv = 80 J/K.mol; b) Cp = 88 J/K.mol; d) U = 80T]
Maximum 4 body, průměr 3,53 bodů (88,2%), s = 0,62, 17 testů.
|
|
8
|
22.10.1999
pátek 7,30'
doba:
18/2 minut
|
Ideální jednoatomový plyn ohřejeme dodáním tepla Q = 1 J. Výchozí tlak, teplota a objem je p0, T0 a V0. Jak se změní teplota
a) Při konstantním tlaku? (2 body)
b) Při konstantním objemu? (2 body)
[a) DT = 2T0/3p0T0 = 0,0026 K; b) DT = 2T0/5p0T0 = 0,0016 K]
Maximum 4 body, průměr 1,35 bodů (33,8%), s = 1,22, 17 testů.
|
|
9
|
22.10.1999
pátek 9,15'
doba:
16/2 minut
|
Ideální plyn má hodnotu Poissonovy konstanty k = 1,1.
a) Kolik stupňů volnosti má jedna molekula? (1 bod)
b) Jaká je hodnota molární tepelné kapacity při konstantním objemu Cv? (1 bod)
c) Jaká je hodnota molární tepelné kapacity při konstantním tlaku Cp? (1 bod)
c) Jaká je vnitřní energie pro n molů tohoto plynu a pro teplotu T? (1 bod)
[a) i = 20; b) Cv = 10 R; b) Cp = 11 R; d) U = 10 nRT]
Maximum 4 body, průměr 3,40 bodů (85,0%), s = 0,51, 15 testů.
|
|
10
|
22.10.1999
pátek 9,15'
doba:
16/2 minut
|
Vzduch (předpokládejte, že je složen z dvouatomových molekul) izochoricky expanduje z objemu V1 = 1 m³ na objem V³ = 2 m³ při talku p = 105 Pa. Výchozí teplota je T1 = 400 K.
a) Jak se změní entropie? (3 body)
b) Jaká je hodnota molární tepelné kapacity za konstantního tlaku Cp? (1 bod)
[DS = 5pV1/2T1.ln2 = 875 ln2 J/K ]
Maximum 4 body, průměr 1,93 bodů (48,3%), s = 1,53, 15 testů.
|
|
11
|
10.11.1999
středa 7,30'
doba:
17/2 minut
|
Matematické kyvadlo kmitá s periodou malých kmitů T = 2 s. Hmotnost závaží je m = 2 kg.
a) Napište pohybovou rovnici. (2 body)
b) Jaká je energie kyvadla pro amplitudu a0 = 0,01 rad? (2 body)
Gravitační zrychlení uvažujete 10 m/s², p² uvažujete jako 10.
[a) a'' + 10 a = 0; b) E = (1/2)mg²a0²(T/2p)² = 0,001 J]
Maximum 4 body, průměr 1,00 bodů (25,0%), s = 0,89, 21 testů.
|
|
12
|
10.11.1999
středa 7,30'
doba:
17/2 minut
|
Fyzikální kyvadlo ve tvaru tyče upevněné otočně na jednom konci kmitá s periodou malých kmitů T = 2 s.
a) Jaká je délka tyče L? (2 body)
b) Jaká je redukovaná délka kyvadla? (2 body)
Gravitační zrychlení uvažujete 10 m/s², p² uvažujete jako 10. Moment setrvačnosti tyče vzhledem k ose procházející kolmo těžištěm je J = 1/12.mL²
[a) L = 3/2 g (T/2p)² = 1,5 m; b) l = g (T/2p)² = 1 m]
Maximum 4 body, průměr 2,62 bodů (65,5%), s = 1,07, 21 testů.
|
|
13
|
10.11.1999
středa 12,45'
doba:
20/2 minut
|
Lineární harmonický oscilátor s tlumením má vlastní frekvenci f = 2 Hz. Logaritmický dekrement útlumu je L = 0,25.
a) Napište pohybovou rovnici oscilátoru. (2 body)
b) Nakreslete přibližně časový průběh kmitů. (2 body)
Poznámka: při kreslení grafu zanedbejte vliv tlumení na skutečnou frekvenci, neboť na cvičení jsme pohybovou rovnici pro tlumený oscilátor neřešili a skutečnou frekvenci jsme nepočítali. Navíc pro malá tlumení jsou obě frekvence blízké (konstanta tlumení vyšla rovna jedné polovině a skutečná frekvence pak vychází 1,9984 Hz.
[a) x'' + x' + 16p² = 0; b) stačilo nakreslit jakýkoliv harmonický průběh s exponenciálním poklesem amplitudy, kde časová konstanta exponenciálního poklesu je rovna čtyřem periodám, tj. 2 s]
Maximum 4 body, průměr 2,29 bodů (57,1%), s = 1,23, 21 testů.
|
|
14
|
10.11.1999
středa 12,45'
doba:
20/2 minut
|
Matematické kyvadlo kmitá s periodou malých kmitů T = 2 s. Hmotnost závaží je m = 2 kg.
a) Napište pohybovou rovnici. (2 body)
b) Jaká je energie kyvadla pro amplitudu a0 = 0,01 rad? (2 body)
Gravitační zrychlení uvažujete 10 m/s², p² uvažujete jako 10.
[a) a'' + 10 a = 0; b) E = (1/2)mg²a0²(T/2p)² = 0,001 J]
Maximum 4 body, průměr 2,52 bodů (63,1%), s = 1,29, 21 testů.
|
|
15
|
19.11.1999
pátek 7,30'
doba:
12/2 minut
|
Vlnová délka harmonické jednodimenzionální vlny šířící se ve směru souřadnice x má vlnovou délku l = 0,1 m. Frekvence je rovna f = 1 kHz a amplituda má hodnotu U0 = 25 (jakýchkoliv jednotek, záleží o jakou jde vlnu).
a) Napište (číselně) vztah pro okamžitou výchylku u(x, t). (2 body)
b) Vypočtěte hodnotu fázové rychlosti vf. (2 body)
[a) jeden z možných zápisů: u(x, t) = 25cos(20px - 2000pt); b) vf = 100 m/s]
Maximum 4 body, průměr 3,75 bodů (93,8%), s = 0,68, 16 testů.
|
|
16
|
19.11.1999
pátek 7,30'
doba:
12/2 minut
|
Fyzikální kyvadlo ve tvaru koule upevněné výkyvně na jejím povrchu má hmotnost 1 kg a poloměr R = 0,1 m.
a) Jaká je úhlová frekvence w pro malé výchylky? (2 body)
b) Jaká je redukovaná délka kyvadla? (2 body)
Gravitační zrychlení uvažujete 10 m/s². Moment setrvačnosti koule vzhledem k ose procházející jejím středem je J = 2/5.mR²
[a) w² = 5g/7R = 500/7 1/s² b) l = 7/5 R =7/50 m]
Maximum 4 body, průměr 3,75 bodů (93,8%), s = 0,77, 16 testů.
|
|
17
|
19.11.1999
pátek 9,15'
doba:
14/2 minut
|
Vlnová délka harmonické jednodimenzionální vlny šířící se ve směru souřadnice x má vlnovou délku l = 0,1 m. Frekvence je rovna f = 1 kHz a amplituda má hodnotu U0 = 25 (jakýchkoliv jednotek, záleží o jakou jde vlnu).
a) Napište (číselně) vztah pro okamžitou výchylku u(x, t). (2 body)
b) Vypočtěte hodnotu fázové rychlosti vf. (2 body)
[a) jeden z možných zápisů: u(x, t) = 25cos(20px - 2000pt); b) vf = 100 m/s]
Maximum 4 body, průměr 3,65 bodů (91,2%), s = 0,86, 17 testů.
|
|
18
|
19.11.1999
pátek 9,15'
doba:
14/2 minut
|
Fyzikální kyvadlo ve tvaru koule upevněné výkyvně na jejím povrchu má hmotnost 1 kg a poloměr R = 0,1 m.
a) Jaká je úhlová frekvence w pro malé výchylky? (2 body)
b) Jaká je redukovaná délka kyvadla? (2 body)
Gravitační zrychlení uvažujete 10 m/s². Moment setrvačnosti koule vzhledem k ose procházející jejím středem je J = 2/5.mR²
[a) w² = 5g/7R = 500/7 1/s² b) l = 7/5 R =7/50 m]
Maximum 4 body, průměr 3,53 bodů (88,2%), s = 1,18, 17 testů.
|
|
19
|
19.11.1999
pátek 11,00'
doba:
14/2 minut
|
Vlnová délka harmonické jednodimenzionální vlny šířící se ve směru souřadnice x má vlnovou délku l = 0,1 m. Frekvence je rovna f = 1 kHz a amplituda má hodnotu U0 = 25 (jakýchkoliv jednotek, záleží o jakou jde vlnu).
a) Napište (číselně) vztah pro okamžitou výchylku u(x, t). (2 body)
b) Vypočtěte hodnotu fázové rychlosti vf. (2 body)
[a) jeden z možných zápisů: u(x, t) = 25cos(20px - 2000pt); b) vf = 100 m/s]
Maximum 4 body, průměr 3,44 bodů (86,1%), s = 1,10, 18 testů.
|
|
20
|
19.11.1999
pátek 11,00'
doba:
14/2 minut
|
Fyzikální kyvadlo ve tvaru koule upevněné výkyvně na jejím povrchu má hmotnost 1 kg a poloměr R = 0,1 m.
a) Jaká je úhlová frekvence w pro malé výchylky? (2 body)
b) Jaká je redukovaná délka kyvadla? (2 body)
Gravitační zrychlení uvažujete 10 m/s². Moment setrvačnosti koule vzhledem k ose procházející jejím středem je J = 2/5.mR²
[a) w² = 5g/7R = 500/7 1/s² b) l = 7/5 R =7/50 m]
Maximum 4 body, průměr 3,94 bodů (98,4%), s = 0,25, 16 testů.
|
|
21
|
1.12.1999
středa 7,30'
doba:
18/3 minut
|
Laserové světlo v laboratoři 413 o výkonu 100 mW osvětluje plošku o velikosti 1 cm².
a) Jaká je amplitoda Poyntingova vektoru S0? (2 body)
b) Jaké jsou amplitudy intenzit elektrického a magnetického pole E0 a H0? (2 body)
[ze vztahů I = S0/2 a e0E0² = m0H0² přibližně vyjde S0 = 2000 W/m², H0 = 2,4 A/m, E0 = 850 V/m]
Maximum 4 body, průměr 2,53 bodů (63,2%), s = 0,77, 19 testů.
|
|
22
|
1.12.1999
středa 7,30'
doba:
18/3 minut
|
Hladina akustického tlaku ve vzdálenosti 10 m od sbíječky je Lp = 60 dB. Jakou hladinu slyší pracovník se sbíječkou, je-li od ní vzdálen 0,5 m? (2 body)
[Lp(0,5 m) = Lp(10 m) + 20 log(r2/r1) = 86 dB]
Maximum 2 body, průměr 1,59 bodů (79,4%), s = 0,80, 17 testů.
|
|
23
|
1.12.1999
středa 7,30'
doba:
18/3 minut
|
Jakou rychlostí se musí přibližovat člověk k orchestru, aby vlivem Dopplerova jevu pozoroval posun v ladění o jeden půltón? (2 body)
Jeden půltón odpovídá poměru frekvencí 1:2^(1/12), rychlost zvuku uvažujte c = 300 m/s.
[v = c(1 - 1/2^(1/12) = 17 m/s]
Maximum 2 body, průměr 1,88 bodů (94,1%), s = 0,49, 17 testů.
|
|
24
|
1.12.1999
středa 12,45'
doba:
30/2 minut
|
Do první Maxwellovy rovnice rot H = j + ¶D/¶t dosaďte řešení ve tvaru rovinné vlny a zjistěte, jaký bude vztah mezi velikostí a fází vektorů H a D.
Při tom předpokládejte lineární a izotropní vodivé prostředí s Ohmovým zákonem ve tvaru j = sE a lineární a izotropní prostředí. (2 body) .
Vyšetřete totéž pro případ velmi dobře vodivého prostředí, tj. kdy s >> ew (2 body).
[úplná rovnice: kxH = (js + ew)E;
rovnice pro fázory: k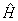 = (js + ew) = (js + ew)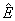 nebo jinak zapsáno s užitím vztahu c = w/k:
nebo jinak zapsáno s užitím vztahu c = w/k: 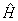 = c(js/w + e) = c(js/w + e)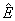 ; vektory E a H nebudou ve fázi, budou fázově posunuty o tg(s/we);
Vztah mezi velikostmi lze napsat např. jako ; vektory E a H nebudou ve fázi, budou fázově posunuty o tg(s/we);
Vztah mezi velikostmi lze napsat např. jako 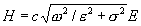 ; v případě dobře vodivého prostředí je ; v případě dobře vodivého prostředí je 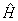 = jcs/w = jcs/w 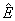 , tj. vektory H a E jsou fázově posunuty o p/2.] , tj. vektory H a E jsou fázově posunuty o p/2.]
Maximum 4 body, průměr 2,10 bodů (52,5%), s = 1,25, 20 testů.
|
|
25
|
1.12.1999
středa 12,45'
doba:
30/2 minut
|
Siréna o akustickém výkonu P generuje čistý tón o frekvenci f.
a) Jaká je ve vzdálenosti r od sirény intenzita zvukových vln? (2 body)
b) Jaká je v téže vzdálenosti hladina akustického tlaku?(2 body)
Referenční hladina akustického tlaku p0 a hustota vzduchu r je zadána.
Nápověda: Intenzita je dána vztahem I = 1/2 rw²U0²vf, kde vf je fázová rychlost zvuku (je to vlastně energie LHO napsaná jako hustota - vlnu si lze představit jako nekonečně mnoho LHO spojitě rozložených v prostoru - násobená fázovou rychlostí, výsledek pak je hustota toku energie), vztah mezi akustickou rychlostí v a akustickým tlakem p je rvvf = p (na cvičení jsme to odvozovali z pohybové rovnice pro kontinuum, protože si však tento vzorec sám nepamatuji, nemohu totéž chtít po studentech), vztah mezi akustickou výchylkou a akustickou rychlostí již nechávám na Vás J .
[Lp(r) = 10 log(2Pvfr/4pr²p0²]
Maximum 4 body, průměr 2,43 bodů (60,7%), s = 1,43, 21 testů.
|
|
26
|
3.12.1999
pátek 7,30'
doba:
30/2 minut
|
Siréna o akustickém výkonu P generuje čistý tón o frekvenci f.
a) Jaká je ve vzdálenosti r od sirény intenzita zvukových vln? (2 body)
b) Jaká je v téže vzdálenosti hladina akustického tlaku?(2 body)
Referenční hladina akustického tlaku p0 a hustota vzduchu r je zadána.
Nápověda: Intenzita je dána vztahem I = 1/2 rw²U0²vf, kde vf je fázová rychlost zvuku (je to vlastně energie LHO napsaná jako hustota - vlnu si lze představit jako nekonečně mnoho LHO spojitě rozložených v prostoru - násobená fázovou rychlostí, výsledek pak je hustota toku energie), vztah mezi akustickou rychlostí v a akustickým tlakem p je rvvf = p (na cvičení jsme to odvozovali z pohybové rovnice pro kontinuum, protože si však tento vzorec sám nepamatuji, nemohu totéž chtít po studentech), vztah mezi akustickou výchylkou a akustickou rychlostí již nechávám na Vás J .
[Lp(r) = 10 log(2Pvfr/4pr²p0²]
Maximum 4 body, průměr 1,61 bodů (40,3%), s = 1,14, 18 testů.
|
|
27
|
3.12.1999
pátek 7,30'
doba:
25/3 minut
|
Hladina akustického tlaku ve vzdálenosti r1 = 10 m od sbíječky je Lp = 60 dB. Jakou hladina akustického tlaku pozoruje pracovník se sbíječkou ve vzdálenosti r2 = 0,5 m? (2 body)
[Lp(r2) = Lp(r1) + 20 log(r1/r2) = 86 dB]
Maximum 2 body, průměr 1,67 bodů (83,3%), s = 0,69, 18 testů.
|
|
28
|
3.12.1999
pátek 7,30'
doba:
25/3 minut
|
Jakou rychlostí se musí přibližovat člověk k orchestru, aby vlivem Dopplerova jevu pozoroval posun v ladění o jeden půltón? (2 body)
Jeden půltón odpovídá poměru frekvencí 1:2^(1/12), rychlost zvuku uvažujte c = 300 m/s.
[v = c(1 - 1/2^(1/12) = 17 m/s]
Maximum 2 body, průměr 2,00 bodů (100,0%), s = 0,00, 19 testů.
|
|
29
|
3.12.1999
pátek 9,15'
doba:
30/3 minut
|
Akustický tlak pozorovaného zvuku je 1000 x větší, než je akustický tlak odpovídající prahu slyšitelnosti p0 = 2.105 Pa.
a) Jaká je hladina akustického talku Lp?(1 bod)
b) Jaká je hodnota intenzity zvuku I?(1 bod)
Nápověda: Intenzita je dána vztahem I = 1/2 rw²U0²vf, kde vf je fázová rychlost zvuku (je to vlastně energie LHO napsaná jako hustota - vlnu si lze představit jako nekonečně mnoho LHO spojitě rozložených v prostoru - násobená fázovou rychlostí, výsledek pak je hustota toku energie), vztah mezi akustickou rychlostí v a akustickým tlakem p je rvvf = p (na cvičení jsme to odvozovali z pohybové rovnice pro kontinuum, vztah mezi akustickou výchylkou a akustickou rychlostí již nechávám bez nápovědy.
Hustotu vyduchu uvažujte přibližně jako r = 1 kg/m3, rychlost zvuku jako v = 300 m/s.
c) Jaká akustická energie je obsažena v 1 m3?(1 bod)
Návod: Všimněte si vzorce pro intenzitu zvuku v předchozím návodu, popř. jejího fyzikálního rozměru.
d) V jaké vzdálenosti se nachází zdroj, je-li jeho akustický výkon P = 100 mW?(1 bod)
[a] Lp(r) = 60 dB; b) I = p²/(2rv) = 2/3.10-6 w/m2; c) W = I/v = 2/9.10-8 J; d) I = P/4pr², z toho r = 109 m]
Maximum 4 body, průměr 3,27 bodů (81,7%), s = 0,70, 15 testů.
|
|
30
|
3.12.1999
pátek 9,15'
doba:
30/3 minut
|
Jakou frekvenci registruje ozorovatel vzdalující se od zdroje zvuku rychlostí v = 30 m/s, vysílá-li zdroj čstý tón o frekvenci 1 kHz? (2 body)
[f' = f(1 - v/c) = 900 Hz]
Maximum 2 body, průměr 2,00 bodů (100,0%), s = 0,00, 15 testů.
|
|
31
|
3.12.1999
pátek 11,00'
doba:
30/3 minut
|
2. Předpokládejme lineární a izotropní prostředí. Proveďme v Maxwellových rovnicích eliminaci např. vektoru H (tak, že první rovnici zderivujeme podle času a z druhé dosadíme za 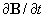 , ke stejnému výsledku dospějeme, aplikujeme-li na druhou Maxwellovu rovnici operátor rotace a z první rovnice dosadíme za rot H ), vztah mezi j a E považujme rovněž za lineární a izotropní, daný Ohmovým zákonem. Obdržíme tak vlnovou rovnici , ke stejnému výsledku dospějeme, aplikujeme-li na druhou Maxwellovu rovnici operátor rotace a z první rovnice dosadíme za rot H ), vztah mezi j a E považujme rovněž za lineární a izotropní, daný Ohmovým zákonem. Obdržíme tak vlnovou rovnici
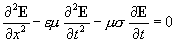 . .
a) Přepište rovnici pro případ rovinné vlny. (2 body)
b) Nalezněte vztah mezi úhlovou frekvencí w a vlnovým číslem k
(tento vztah se nazývá disperzní relace), zjistěte, zda se prostředím může šířit elektromagnetická vlna, popř. fázovou rychlost.
(2 body)
Nápověda: Do rovnice dosaďte řešení ve tvaru monochromatické vlny v exponenciálním tvaru, derivace podle x a t se pak napíšou jako násobení jk a -jw (tak, jak jsme si to ukazovali na cvičení). Existuje-li řešení ve tvaru (netlumené) vlny, musí být w i k reálné.
[a) -k²E = jwmsE + mew²E; b) -k² = jw.ms + mew², nemůže být současně k a w reálné číslo, vlna bude tlumneá]
Maximum 4 body, průměr 1,53 bodů (38,3%), s = 1,68, 15 testů.
|
|
32
|
3.12.1999
pátek 11,00'
doba:
30/3 minut
|
Jakou frekvenci registruje ozorovatel vzdalující se od zdroje zvuku rychlostí v = 108 km/h, vysílá-li zdroj čstý tón o frekvenci 1 kHz? (2 body)
[f' = f(1 - v/c) = 900 Hz]
Maximum 2 body, průměr 2,00 bodů (100,0%), s = 0,00, 16 testů.
|
|
33
|
3.12.1999
pátek 11,00'
doba:
30/3 minut
|
Hladina akustického tlaku ve vzdálenosti r1 = 10 m od sbíječky je Lp = 60 dB. Jakou hladina akustického tlaku pozoruje pracovník se sbíječkou ve vzdálenosti r2 = 0,5 m? (2 body)
[Lp(r2) = Lp(r1) + 20 log(r1/r2) = 86 dB]
Maximum 2 body, průměr 1,81 bodů (90,6%), s = 0,40, 16 testů.
|
|
34
|
15.12.1999
středa 7,30'
doba:
25/2 minut
|
Krátkozraké oko má daleký bod ve vzdálenosti 0,75 m.
a) Vypočtěte ohniskovou vzdálenost brýlových skel pro koreci krátkozrakosti. (2 body)
b) Nakreslete obrázek, s uvažováním znaménkové konvence. (1 bod)
c) Spočítejte optickou mohutnost čočky. (1 bod)
[a) f = -0,75 m, jde tedy o rozptylku; c) D = 1/f = -4/3 Dioptrie]
Maximum 4 body, průměr 3,50 bodů (87,5%), s = 0,52, 16 testů.
|
|
35
|
15.12.1999
středa 7,30'
doba:
25/2 minut
|
Polovina rovnoběžného monochromatického světelného svazku prochází optickou destičkou s indexem lomu n = 1,5, druhá polovina prochází mimo destičku. Vlnová délka je l = 500 nm.Spočítejte šířku destičky d tak, aby v bodě, kde soustředíme všechny paprsky svazku (např. parabolickým zrcadlem) došlo k interferenčnímu maximu. (4 body)
[dn - d = kl, z toho d = kl/(n - 1) = k.1 mm (je nekonečně mnoho řešení, k je celé číslo - řád interference)]
Maximum 4 body, průměr 1,88 bodů (46,9%), s = 1,36, 16 testů.
|
|
36
|
15.12.1999
středa 12,45'
doba:
20/2 minut
|
Krátkozraké oko má daleký bod ve vzdálenosti 0,75 m.
a) Vypočtěte ohniskovou vzdálenost brýlových skel pro koreci krátkozrakosti. (2 body)
b) Nakreslete obrázek, s uvažováním znaménkové konvence. (1 bod)
c) Spočítejte optickou mohutnost čočky. (1 bod)
[a) f = -0,75 m, jde tedy o rozptylku; c) D = 1/f = -4/3 Dioptrie]
Maximum 4 body, průměr 3,00 bodů (75,0%), s = 0,69, 18 testů.
|
|
37
|
15.12.1999
středa 12,45'
doba:
20/2 minut
|
Duté zrcadlo má poloměr r = 1 m. Předmět je ve vzdálenosti a = -20 cm.
a) Nakreslete obrázek podle znaménkové konvence s chodem alespoň dvou význačných paprsků. (1 bod)
b) Vypočtěte polohu obrazu. (1 bod)
c) Jaké je zvětšení Z? (1 bod)
d) Jde o obraz skutečný nebo neskutečný? (1 bod)
[b) a' = 1/(2/r - 1/a) = 1/3 m ; c) Z = -a'/a -= 5/3; d) obraz je neskutečný]
Maximum 4 body, průměr 3,67 bodů (91,7%), s = 0,69, 18 testů.
|
|
38
|
7.1.2000
doba:
15/2 minut
|
Opravný test:
Ideální plyn změní objem z hodnoty V1 na hodnotu V2 při konstantní teplotě T.
a) Jakou práci systém vykoná? (2 body)
b) Jak se změní vnitřní energie plynu? (1 bod)
c) Jaké teplo se při tomto dějí musí plynu dodat? (1 bod)
[a) A = nRln(V2/V1); b) DU = 0 … jde o izotermický děj; c) Q = A]
Maximum 4 body, průměr 4,00 bodů (100,0%), s = 0,00, 1 testů.
|
|
39
|
7.1.2000
doba:
15/2 minut
|
Opravný test:
Ideální plyn má hodnotu Poissonovy konstanty k = 1,1.
a) Kolik stupňů volnosti má jedna molekula? (1 bod)
b) Jaká je hodnota molární tepelné kapacity při konstantním objemu Cv? (1 bod)
c) Jaká je hodnota molární tepelné kapacity při konstantním tlaku Cp? (1 bod)
c) Jaká je vnitřní energie pro n molů tohoto plynu a pro teplotu T? (1 bod)
[a) i = 20; b) Cv = 10 R; b) Cp = 11 R; d) U = 10 nRT]
Maximum 4 body, průměr 4,00 bodů (100,0%), s = 0,00, 1 testů.
|
|
40
|
7.1.2000
doba:
15/2 minut
|
Opravný test:
Hladina akustického tlaku ve vzdálenosti 10 m od sbíječky je Lp = 60 dB. Jakou hladinu slyší pracovník se sbíječkou, je-li od ní vzdálen 0,5 m? (2 body)
[Lp(0,5 m) = Lp(10 m) + 20 log(r2/r1) = 86 dB]
Maximum 2 body, průměr 2,00 bodů (100,0%), s = 0,00, 1 testů.
|
|
41
|
7.1.2000
doba:
15/2 minut
|
Opravný test:
Siréna o akustickém výkonu P generuje čistý tón o frekvenci f.
a) Jaká je ve vzdálenosti r od sirény intenzita zvukových vln? (2 body)
b) Jaká je v téže vzdálenosti hladina akustického tlaku?(2 body)
Referenční hladina akustického tlaku p0 a hustota vzduchu r je zadána.
Nápověda: Intenzita je dána vztahem I = 1/2 rw²U0²vf, kde vf je fázová rychlost zvuku (je to vlastně energie LHO napsaná jako hustota - vlnu si lze představit jako nekonečně mnoho LHO spojitě rozložených v prostoru - násobená fázovou rychlostí, výsledek pak je hustota toku energie), vztah mezi akustickou rychlostí v a akustickým tlakem p je rvvf = p (na cvičení jsme to odvozovali z pohybové rovnice pro kontinuum, protože si však tento vzorec sám nepamatuji, nemohu totéž chtít po studentech), vztah mezi akustickou výchylkou a akustickou rychlostí již nechávám na Vás J .
[Lp(r) = 10 log(2Pvfr/4pr²p0²]
Maximum 4 body, průměr 2,00 bodů (50,0%), s = 0,00, 1 testů.
|
|
42
|
7.1.2000
doba:
6 minut
|
Opravný test:
Hladina akustického tlaku ve vzdálenosti r1 = 10 m od sbíječky je Lp = 60 dB. Jakou hladina akustického tlaku pozoruje pracovník se sbíječkou ve vzdálenosti r2 = 0,5 m? (2 body)
[Lp(r2) = Lp(r1) + 20 log(r1/r2) = 86 dB]
Maximum 2 body, průměr 2,00 bodů (100,0%), s = 0,00, 1 testů.
|
|
43
|
7.1.2000
doba:
6 minut
|
Opravný test:
Krátkozraké oko má daleký bod ve vzdálenosti 0,75 m.
a) Vypočtěte ohniskovou vzdálenost brýlových skel pro koreci krátkozrakosti. (2 body)
b) Nakreslete obrázek, s uvažováním znaménkové konvence. (1 bod)
c) Spočítejte optickou mohutnost čočky. (1 bod)
[a) f = -0,75 m, jde tedy o rozptylku; c) D = 1/f = -4/3 Dioptrie]
Maximum 4 body, průměr 1,00 bodů (25,0%), s = 0,00, 1 testů.
|