Pozoruhodná haló jádra

Filip Křížek, 5. září 2005

Díky moderní urychlovačové technice jsme schopni připravit si nejrozmanitější exotické izotopy známých prvků. Stále častěji se nám tak daří pronikat do velmi vzdálených a dosud neprobádaných oblastí údolí stabiltyÚdolí stability – je také někdy nazýváno údolím nuklidů. Jedná se o třírozměrný graf, v němž u známých izotopů všech prvků vynášíme na osu x počet neutronů, na osu y počet protonů a na osu z záporně vzatou průměrnou vazbovou energii na jeden nukleon. daleko od jeho dna. Nemůžeme se proto divit, když na samém jeho okraji objevujeme u jader pozoruhodné a zcela nečekané vlastnosti. Už od poloviny 80. let minulého století se fyzikové setkávají u izotopů lehkých prvků, které mají extrémní poměr počtu protonů k počtu neutronů, s tzv. haló. O co se jedná? Běžná jádra si můžeme představit jako malinkou kapičku nukleonové kapaliny. U haló jader si tímto přiblížením nevystačíme. Spíše bychom je mohli popsat jako kompaktní centrální objekt (jadérko), kolem kterého se do dálky rozprostírá oblak slabě vázaných nukleonů (haló). Celý tento systém proto vypadá spíše jako jakási „jaderná molekula“.

Jak vypadají jádra blízko dna údolí stability

Dříve než se budeme zabývat jádry s protonovým nebo neutronovým haló, připomeňme si některá základní fakta týkající se jader a jejich popisu.

V jádře je soustředěna většina hmoty atomu, v porovnání s ním má však pouze velice malý rozměr. Silná interakce v něm váže dohromady protony a neutrony, které kvůli jejich podobnému chování souhrnně označujeme jako nukleonyNukleon – částice jádra, baryon složený z kvarků u a d. Jde protony a neutrony. . Všechny nukleony jsou fermionyFermiony – částice, které mají poločíselný spin, vlnová funkce je antisymetrická, splňují Pauliho vylučovací princip a podléhají Fermiho–Diracovu statistickému rozdělení. Patří mezi ně všechny leptony, kvarky a baryony – například elektron, neutrino, proton, neutron. Při nízkých teplotách fermiony obsazují stavy postupně, až po tzv. Fermiho mez E_F., a proto se řídí Pauliho vylučovacím principemPauliho vylučovací princip – „Dva fermiony nemohou být nikdy ve stejném kvantovém stavu". Právě proto různé elektrony v atomárním obalu zaujímají různé kvantové stavy a tím vytvářejí různorodé chování chemických prvků. . V jádře tedy nenalezneme dva neutrony, popřípadě protony, které by měly všechna kvantová čísla stejná.

Otázkou, jak jsou jádra vlastně velká, se zabýval již Ernest Rutherford v roce 1911, když studoval rozptyl alfa částic na jádrech zlata. Daleko přesnější představu o jejich rozměrech a stavbě jsme však získali až v padesátých letech dvacátého století, kdy Robert Hofstadter prováděl svoje slavné experimenty na urychlovači ve Standfordu. Místo alfa částic použil jako rozptylovou sondu elektrony. To mu umožnilo studovat rozložení elektrického náboje v jádře. Potvrdil, že jádra mají konečný rozměr, zároveň je ale jejich hranice neostrá. Na Obr. 1 můžeme pozorovat, jak vypadají typické průběhy hustoty v jádrech. V samotném centru je hustota téměř konstantní, v povrchové oblasti pak postupně klesá až na nulu.

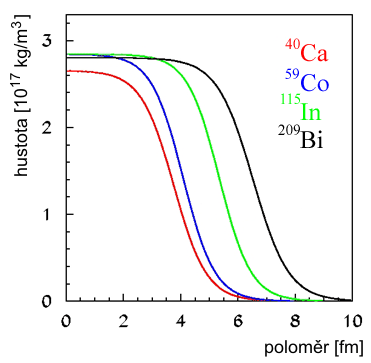
Obr. 1: Rozdělení hustoty v jádrech, převzato z [4].

Z Obr. 1 je také vidět, že centrální hustoty v jádrech jsou přibližně stejné. Tento fakt vysvětlujeme efektem tzv. nasycení (saturace) jaderných sil. Každý nukleon může díky jejich krátkému dosahu interagovat pouze s omezeným počtem okolních nukleonů. Pro poloměr jádra s A nukleony pak přibližně platí

R_J = r ₀A ^1/3,

kde r ₀ je empirická konstanta rovná 1,2 fm.

Hmotnost jader není rovna prostému součtu hmotností jeho protonů a neutronů. Ještě je totiž nutno uvážit záporný příspěvek vazbové energie, o který se nukleony ochudily, když dohromady vytvořily stabilnější vázaný systém. Označíme-li symbolem B(A, Z) vazbovou energii jádra s A nukleony a Z protony, pak platí

B(A, Z) = ZM_pc² + (A−Z)M_nc² − M_J(A, Z)c²,

kde M_p, resp. M_n je klidová hmotnost protonu, resp. neutronu, M_J(A, Z) klidová hmotnost příslušného jádra a c rychlost světla ve vakuu. Závislost vazbové energie jádra na počtu a zastoupení nukleonů vystihuje semiempirická Weizsäckerova formule:

B(A, Z) = a_VA − a_SA^2/3 − a_CZ²/A^1/3 − a_SYM (A−2Z)²/A + d(A),

kde a_V, a_S, a_C a a_SYM jsou kladné konstanty. První člen ve formuli, tj. a_VA, se nazývá objemový. Započítáváme jím efekt nasycení jaderných sil. Každý nukleon v centrální oblasti přispívá k vazbové energii stejným dílem. Nukleony, které jsou na povrchu jádra, nejsou ale tak dobře vázány jako nukleony v centrální oblasti. Tuto skutečnost v sobě odráží tzv. povrchový člen a_SA^2/3. Vazbovou energii snižuje i coulombické odpuzování protonů, a_CZ²/A^1/3. Podstatnou roli hraje také poměr, v jakém jsou protony a neutrony v jádře zastoupeny. Pokud budeme do jádra přidávat neustále pouze protony (nebo neutrony), pak je díky Pauliho vylučovacímu principu budeme muset umisťovat na stále vyšší a vyšší energetické hladiny. Dostávali bychom se tak do energeticky nevýhodných konfigurací. Symetrizační člen, a_SYM(A−2Z)²/A, proto upřednostňuje ta jádra, která mají podobný počet protonů a neutronů. Ještě je třeba osvětlit význam posledního členu d(A). Ten zohledňuje efekt tzv. párování. Jádra jsou lépe vázána, jsou-li sudo-sudá, tj. pokud mají sudý počet protonů i neutronů. Sudo-liché nebo licho-liché kombinace jsou vázány hůře.

Z Weizsäckerovy formule je vidět, že pro konstantní počet nukleonů bude vazbová energie kvadratickou funkcí počtu protonů Z. Díky tomu má řez údolím stability podél linie A = konst. liché zhruba profil paraboly, viz Obr. 2. Pro A = konst. sudé je situace o něco komplikovanější. Rozpadem sudo-sudého jádra totiž dostaneme jádro licho-liché a naopak. Do celkové energetické bilance se v tomto případě promítne i vliv párovacího členu. Ten dodatečně posune energii základního stavu u jader sudo-sudých níže než u licho-lichých kombinací. Díky tomu dostaneme dvě různé paraboly.

Jádra na úbočích údolí stability přecházejí posloupností beta rozpadů (β⁻ nebo β⁺) popřípadě elektronových záchytů (EC) do co možná nejstabilnější konfigurace. Povšimněme si také, že směrem ke dnu údolí se výrazně prodlužují poločasy přeměn.

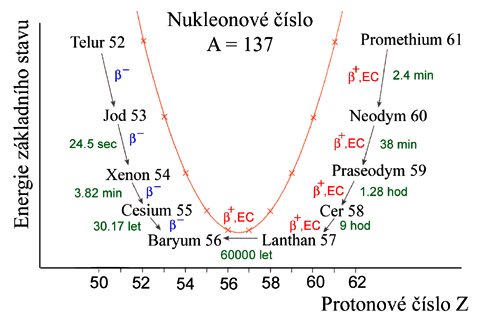
Obr. 2: Profil údolí stability za podmínky, že počet nukleonů je lichý a neměnný,
převzato z [1].

Pokud u všech existujících izotopů známých prvků zaznamenáme jejich polohy do grafu protonové číslo (Z) versus počet neutronů (N), dostaneme Obr. 3. Je to pohled na údolí stability shora. Černá pole označují stabilní izotopy tvořící jeho dno. Ostatní jádra jsou radioaktivní. Údolí je ohraničeno několika liniemi, které vymezují limity existence jader jako vázaných systémů. Zelená čára je mezí stability vůči spontánnímu rozštěpení. Jádra za touto hranicí se vlivem coulombického odpuzování protonů okamžitě rozštěpí a nevytvoří ani vázaný stav. Nás budou ale spíše zajímat linie s označením S_n = 0 a S_p = 0. Určují totiž, u kterých izotopů je energie potřebná na odebrání neutronu, respektive protonu nulová. Tyto linie se proto nazývají liniemi přesycenosti (drip line) a právě poblíž nich se u lehkých prvků setkáváme s haló jádry.

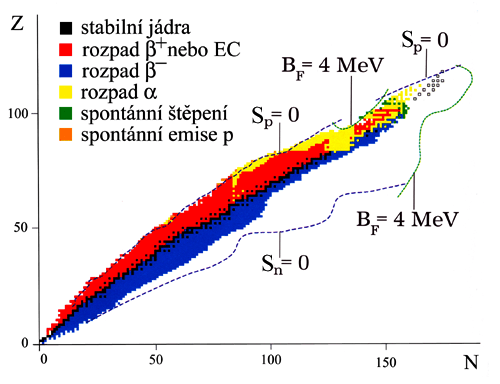
Obr. 3: Údolí stability, převzato z [1].

Co je to haló?

V makrosvětě se s tímto pojmem setkáváme například v astronomii nebo meteorologii. Většinou jím myslíme řídkou nebo méně intenzivní obálku rozprostírající se kolem nějakého hmotného nebo jasného centrálního objektu. Profesor A. S. Jensen a jeho spolupracovníci se ve svém přehledovém článku [2] zabývali tím, jak zavést pojem haló do mikrosvěta. Většinou jím chceme vyjádřit to, že nějaký kvantový objekt (jádro, atom nebo molekula) má daleko větší rozměry, než bychom čekali. Definice uvedená ve výše zmíněném přehledovém článku se opírá o pojem mnohočásticové vlnové funkce systému a ve zjednodušené formě říká:

U kvantového objektu hovoříme o tom, že vykazuje haló strukturu, jestliže jsou současně splněny následující podmínky:

1. je veliká pravděpodobnost(> 0,5), že najdeme celý systém rozdělený na vzájemně slabě vázané podsystémy,
2. s velikou pravděpodobností (> 0,5) lze také nalézt systém v konfiguraci, kdy jsou jednotlivé podsystémy rozmístěny v klasicky zakázaných oblastech, tj. mimo dosah vzájemného působení.

Tato definice zajišťuje, že pojem haló není závislý na detailech dvoučásticových efektivních interakcí a velikosti rozměrové škály. Objekty, které splňují předchozí podmínky, vděčí za svoji existenci pouze kvantové mechanice, respektive chovaní své vlnové funkce na velikých vzdálenostech.

Uveďme alespoň jeden zajímavý příklad haló stavu na atomární úrovni. Je známo, že inertní plyny netvoří za normálních podmínek molekuly. Poměrně nedávno se však zjistilo, že dva atomy ⁴He vázaný stav vytvořit mohou. Jeho vazbová energie je však neuvěřitelně malá (okolo 1,3×10⁻⁷ eV). Rozměr tohoto systému je 5,2 nm, tedy daleko větší než velikost obyčejné dvouatomové molekuly. Podobný systém sestávající z ⁴He a ³He je ale nevázaný.

Haló jádra

Skutečnost, že některá jádra mohou vykazovat haló strukturu, není vlastně zase tak novým zjištěním. Poprvé se s tímto jevem setkali fyzikové už u deuteronu – jádra těžkého vodíku. Jedná se o slabě vázaný systém (B = 2,2 MeV) protonu a neutronu, přičemž jejich vzájemná vzdálenost je asi 4 fm. Dosah jaderných sil je ale pouze 1,2÷1,4 fm. U deuteronu je tudíž veliká pravděpodobnost, že najdeme proton a neutron od sebe dále, než je dosah jejich interakce.

Do opravdového středu zájmu se dostala haló jádra až v osmdesátých létech 20. století. Tehdy se zjistilo, že účinný průřezÚčinný průřez – vhodný způsob vyjádření pravděpodobnosti, že ostřelující částice bude jistým způsobem interagovat s částicí terče. V podstatě jím zobrazujeme každou částici terče jako určitou malou plochu nastavenou dopadajícím částicím. Všechny částice, které směřují na tuto plochu, interagují. Pravděpodobnost interakce tedy roste s velikostí účinného průřezu. pro interakci izotopů lithia s terčem výrazně vybočoval u ¹¹Li. Celkem brzy byl tento efekt kvalitativně vysvětlen tím, že kolem jádra ⁹Li obíhají dva velmi slabě vázané valenční neutrony. Energie potřebná k jejich odtržení od zbytku systému je pouze 0,3 MeV. Pro porovnaní uveďme, že jádra ze dna údolí stability mají většinou vazbovou energii okolo 8,5 MeV na nukleon.

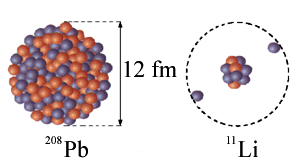
Obr. 4: Lithium 11 má dva slabě vázané valenční neutrony.
Rozměr haló, které vytvářejí kolem centrálního jadérka,
je srovnatelný s velikostí jádra olova 208. Převzato z [3].

Postupem času byla nalezena haló struktura také u dalších jader. Navíc se zjistilo, že se jí mohou pochlubit i některé excitované stavy nebo exotická jádra. Například takový hypertriton ³_ΛH si lze přestavit jako deuteron, k němuž je velmi slabě vázána částice ΛLambda částice – jedna z částic objevených v kosmickém záření. Její kvarková struktura je uds, tedy jde o baryon obsahující podivný kvark. Částice nemá elektrický náboj, proto za sebou nezanechává v mlžné komoře žádnou stopu, dokud se nerozpadne pomocí slabé interakce, většinou na proton a záporný pion. Proton a pion za sebou zanechávají stopu ve tvaru písmene Λ, která dala částici její jméno. . K tomu, abychom ji od zbytku systému separovali, musíme vynaložit pouze 0,14 MeV. Příklady jader, u nichž se setkáváme s nukleonovým haló, naleznete na Obr. 5.

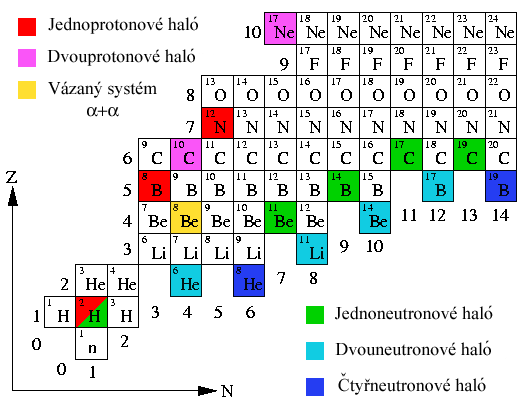
Obr. 5: Dolní okraj údolí stability. Barevná pole označují, která jádra
vykazují haló strukturu v základním stavu. Deuteron ² H je vázaný stav protonu
a neutronu, proto stojí na pomezí dvou skupin. Data pocházejí z [2].

Borromejská jádra

Tato skupina haló jader dostala své jméno podle italské rodiny Borromeo. V jejím erbovním znamení se totiž vyskytuje pozoruhodná spleť tří kroužků svázaných dohromady. Přetneme-li však libovolný z nich, budou ostatní dva také volné. Jako borromejská jádra tedy označujme ta, která můžeme popsat jako vázaný systém složený ze tří částí. Přitom žádné dva podsystémy nevytvoří samy o sobě vázaný stav. Typickým zástupcem této rodiny jader je helium 6. Lze ho popsat jako alfa částici, kolem které obíhají dva slabě vázané neutrony. Avšak ani ⁵He ani systém dvou neutronů neexistují v přírodě jako vázané. U borromejských jader se tedy setkáváme s projevy tříčásticových sil.

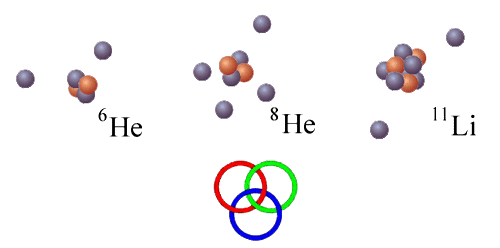
Obr. 6: Příklady borromejských jader. Stejně jako ⁶He patří do této skupiny i ⁸He.
Můžeme se na něj totiž dívat jako na systém sestávající z ⁶He a dvou neutronů.
Ve spodní části obrázku jsou nakresleny borromejské kroužky.

Jak vlastně zkoumáme haló strukturu jádra?

Předně musíme říci, že drtivá většina haló jader má poločasy rozpadu v rozmezí milisekund až sekund. Z tak krátce žijícího izotopu si však jen těžko vyrobíme nějaký terčík, na kterém bychom následně mohli provádět rozptyl částic. Proto se hledala jiná cesta. Řešení tohoto problému se ukázalo být překvapivě prosté. Nejdříve svazkem stabilních těžkých jader ostřelujeme tenký terčík z lehkého prvku. Přitom se produkují nejrůznější fragmenty, které vylétají ven. Vzácně se pak mezi nimi může objevit i hledané haló jádro. Abychom jej oddělili od ostatních produktů, necháme všechny fragmenty procházet hmotnostním separátorem. Tím získáme čistý svazek haló jader, který je možno zacílit na druhý terčík.

Vlastnosti haló jader se dají zkoumat různými způsoby. Energie potřebné na jejich rozbití jsou velice malé. Přitom jednotlivé podsystémy vykazují úzká rozdělení hybností. Z Heisenbergova principu neurčitosti vyplývá, že tomu odpovídá široká prostorová distribuce valenčních nukleonů. Díky tomu je také celkový účinný průřez pro interakci u haló jader o mnoho větší než u jader se stejným počtem nukleonů.

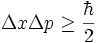
Obr. 7: Relace neurčitosti mezi hybnostním a prostorovým rozlišením.

Nukleonové haló také nepatrně mění tvar elektrického potenciálu jádra, což trochu ovlivňuje i energie hladin v elektronovém obalu. Oproti stabilnímu izotopu pak pozorujeme posun čar ve spektru. To nám zpětně umožňuje něco říci o prostorovém rozmístění valenčních nukleonů.

Výzkum haló jader má i některé důležité astrofyzikální aplikace. Jako příklad uveďme izotop ⁸B, který se účastní procesu slučování vodíku ve Slunci. Vzhledem k tomu, že na produkci haló jader nejsou zapotřebí žádné závratně veliké energie, je možnost jejich studia dostupná širokému okruhu urychlovačů po celém světě. Mezi nejdůležitější centra, která se výzkumem haló jader zabývají, patří francouzský GANIL, německé GSI Darmstadt nebo švýcarský CERN.

Bonus: Animace „Srážka dvou jader zlata“

V animaci vidíte výsledek čelní srážky dvou jader zlata urychlených na energii 200 GeV. Animace byla vytvořena pomocí snímků nabitých částic při skutečném experimentu na detektoru STAR urychlovače RHIC (Relativistic Heavy Ion Collider) v Brookhavenské národní laboratoři na Long Islands. V animaci je patrné, že detektor má válcový tvar. Na urychlovači RHIC probíhá intenzivní výzkum kvark-gluonového plazmatu, které vzniká při podobných srážkách.

Odkazy