Ultrazvukové vlny pohybující se nadsvětelnou rychlostí

Stanislav Poddaný, 28. 11. 2005

Zvukem nazýváme každé mechanické vlnění v látkovém prostředí, které je schopno vyvolat v lidském uchu vjem. Frekvence zvuku je zhruba v rozmezí 16 Hz ÷ 20 kHz. Mechanické vlnění s frekvencí nižší než 16 Hz označujeme za infrazvuk, s frekvencí vyšší než 20 kHz za ultrazvuk. Rychlost šíření zvuku závisí na prostředí, ve kterém se vlnění pohybuje, a na jeho teplotě. Ve vzduchu pro ni platí přibližný vzorec v_z = (331,82 + 0,61 t) m·s⁻¹, kde teplota t je ve °C. To je v porovnání s rychlostí světla ve vakuu 300 000 km·s⁻¹ rychlost zanedbatelná.

Při studiu vlnových jevů v prostředích s disperzí (prostředí, kde závisí index lomu n = c/v na vlnové délce, resp. frekvenci) se setkáváme se dvěma typy rychlostí, s fázovou rychlostí a s grupovou rychlostí.

Fázová rychlost popisuje rychlost šíření ploch se stejnou fází. Nesouvisí se skutečným makroskopickým přesunem hmoty. Typickým příkladem jsou kruhy na vodní hladině vzniklé po vhození kamene. Vzniklé vlny šířící se po hladině nic nevypovídají o rychlosti, s jakou se přesouvají reálné částice vody, ty se pohybují přibližně po elipse a zůstávají stále v okolí téhož místa. Fázová rychlost může nabývat hodnot i vyšších než 300 000 km·s⁻¹, aniž by byly porušeny zákony fyziky, protože nekonečně dlouhá řada vln o konstantní amplitudě nemůže nést „signál“,

v_f(ω) = c/n(ω).

Oproti tomu grupová rychlost představuje rychlost přesunu vlnového balíku – klubka vln podobných frekvencí a vlnových délek. Tato rychlost poukazuje na rychlost přesunu energie a nutně musí být podsvětelná,

v_g(ω) = c/[n(ω)+dn/dω].

Při vlnění bez disperze se všechny postupné vlny šíří stejnou fázovou rychlostí, tedy i libovolný „signál“, který z nich složíme, se šíří touž rychlostí bez změny tvaru (fázová rychlost odpovídá rychlosti grupové). Naproti tomu při vlnění s disperzí se postupné vlny různých frekvencí vlivem rozdílných fázových rychlostí proti sobě posouvají, a tím se signál rozplývá (fázová rychlost obecně není rovna rychlosti grupové). Zvuk hromu, který slyšíme z dálky, je proto „měkký“, zatímco z blízka bychom ho slyšeli jako ostrý praskot.

Joel Mobley z Mississippské univerzity spolu se svým týmem poukázal na způsob, kterým lze zvýšit rychlost ultrazvuku ve vodě z obvyklých 1 500 m·s⁻¹ na rychlosti nejen blízké rychlosti světla, ale až na rychlosti vyšší než rychlost světla ve vakuu, a tím i překonání vzdálenosti v „záporném čase“.

Z výpočtů a simulací provedených Mobleyovou skupinou je patrné, že pro prudké zvýšení rychlosti ultrazvukových vln je zapotřebí vytvoření silně disperzní směsi (voda + plastová zrnka o průměru 0,1 mm). Do takto připravené směsi (100:1) byla poslána ultrazvuková vlna modulovaná do tvaru dvojitého zvonu (viz Obr. 1) o frekvenci 1÷15 MHz.

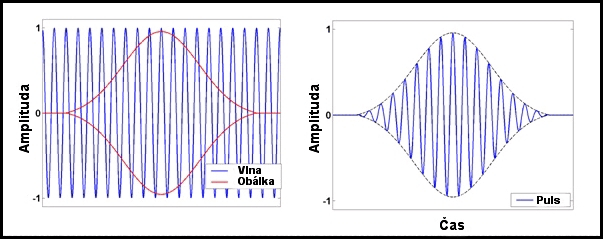
Obr. 1: Vlna s modulací ve tvaru zvonu.

Výsledek experimentu ukazuje graf na Obr. 2. V oblastech frekvencí blízkých 7 MHz dochází k zvýšení fázové rychlosti a výraznému tlumení amplitudy signálu.

Obr. 2: Výsledek experimentu. Závislost koeficientu tlumení a fázové rychlosti na frekvenci.

Mobley dále zjistil, že pro dosažení světelné rychlosti ultrazvukových vln je zapotřebí utvořit směs, která obsahuje přibližně 400 000 zrnek v 8 ml vzorku. Přidáním pouhých 4 zrnek vzroste rychlost nejen nad rychlost světla, ale stane se zápornou (v tom smyslu, že vzdálenější detektor detekuje maximální amplitudu obálky dříve než detektor bližší). Simulace průchodu vln takovýmto prostředím ukazuje graf na Obr 3.

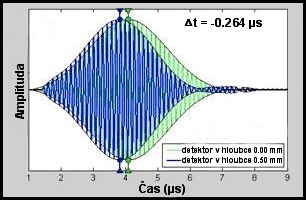
Obr. 3: Simulace průchodu vln disperzní směsí.

Modrá barva představuje signál zachycený přijímačem, který byl umístěn hlouběji v disperzní směsi. Při prohlídce grafu si nelze nepovšimnout, že přijímač umístěný ve větší hloubce zaznamenal vrchol signálu dříve než přijímač blíže povrchu. To je jako prohodit cihlu oknem a pozorovat dříve její dopad a teprve až pak rozbití skla. Jak je to možné? Problém spočívá v naší představě, jak se vlna pohybuje a v klasickém vnímání času. V takovémto případě musíme rozlišovat skutečný přesun vrcholu vlny prostorem a časový záznam detektoru v určitém místě. Může se to zdát překvapivé, ale vlny se nechovají tak jako klasické cihly, se kterými máme každodenní zkušenosti.

Přestože se vrchol vlny pohybuje nadsvětelnou rychlostí, nedochází k porušení zákona kauzalityKauzalita – příčinná souvislost. Pokud jsou dva děje v příčinné souvislosti (například zapálení rozbušky a exploze) musí ve všech souřadnicových soustavách nastat ve stejném pořadí.. Grafy na Obr. 4 ukazují, že čelo signálu, které je odpovědné za přenos informace, se pohybuje „obyčejnou“ rychlostí. Čelo signálu je prvně zaznamenáno přijímačem, který je umístěn v menší hloubce, teprve vrchol se pohybuje nadsvětelně. Se zvyšující se nadsvětelnou rychlostí (větší hloubkou proniknutí signálu do disperzního prostředí) dochází k exponenciálnímu tlumení signálu a jeho deformaci. Právě toto výrazné tlumení bude velkou překážkou k experimentálnímu ověření nadsvětelného pohybu ultrazvukových vln. V každém případě nadsvětelný puls zanikne ještě dříve, než stačí poslat informaci rychleji než světlo. Zákony relativity i tentokráte obstály.

Obr. 4: Šíření signálu, záznam obou detektorů.

Animace k tomuto bulletinu

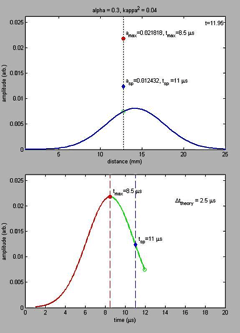
Netlumený pulz se šíří prostředím. Přerušovaná čára znázorňuje pozici detektoru, v dolní části záznam nahraný detektorem v čase.	Tlumený pulz se pohybuje prostředím. Přerušovaná čára znázorňuje pozici detektoru, v dolní části je záznam nahraný detektorem v čase. Maximum zaznamenané detektorem je jiné než pozice maxima pohybujícího se prostředím.
Pohyb pulzu, který prošel do disperzního prostředí a záznam nahraný dvěma detektory (zelený je těsně za rozhraním, modrý dále v disperzním prostředí). Nepřerušovaná čára je rozhraní mezi vodou a disperzí. Přerušované čáry označují pozice detektorů.	Stejná animace jako v předchozím případě, ale pro „nadsvětelný režim“. Čelo pulzu nesoucí informaci se ke vzdálenějšímu detektoru (modrému) dostane později ve shodě se zákonem kauzality. Maximum záznamu je na vzdálenějším detektoru (modrém) ovšem dříve než na záznamu pořízeném bližším detektorem (zeleným). Jde ale o čistě geometrický efekt záznamu nahraného v místě detektoru.

Odkazy