| Poř. |
Datum |
Zadání |
|
1
|
30.3.1999
úterý 12,45'
doba:
8 minut
|
1. Automobil se pohybuje se zrychlením a = -2 m/s2 .
a) Za jak dlouho se zastaví? (1 bod)
b) Jakou urazí dráhu? (1 bod)
2. Přes pevnou kladku visí nehmotné lano, na jehož koncích jsou připevněna závaží o hmotnosti m1 a m2. Napište pohybovou rovnici. (1 bod)
[1. a) t = 12 s; b) s = 144 m; 2. (m1 - m2).g = (m1 + m2).a]
Maximum 3 body, průměr 2,37 bodů (78,9%), s = 0,44, 19 testů.
|
|
2
|
30.3.1999
úterý 16,15'
doba:
9 minut
|
1. Těleso vystřelíme svisle vzhůru rychlostí v0 = 100 m/s.
a) Jaká bude rychlost tělesa za dobu 3 s? (1 bod)
b) Jaká bude maximální výška tělesa? (1 bod)
c) Za jak dlouho dopadne těleso zpět na zem? (1 bod)
Gravitační zrychlení uvažujte g = 10 m/s2.
[a) v (t = 3 s) = 70 m/s; b) hmax = 500 m; c) t = 20 s]
Maximum 3 body, průměr 2,81 bodů (93,8%), s = 0,48, 24 testů.
|
|
3
|
30.3.1999
úterý 18,00'
doba:
8 minut
|
1. Do studny pustíme kamínek. Dopad do vody uslyšíme za 4 sekundy (zpoždění v důsledku konečné rychlosti zvuku zanedbejte).
a) Jak hluboká je studna? (1 bod)
b) Jakou rychlostí kamínek dopadl? (1 bod)
Gravitační zrychlení uvažujte g = 10 m/s2.
2. Napište (vektorovou) pohybovou rovnici pro těleso pohybující se volně v homogenním gravitačním poli nad zemským povrchem. Uvažujte dvě dimenze, souřadnice x je rovnoběžná se zemským povrchem, souřadnice y směřuje kolmo vzhůru. (1 bod)
[1. a) h = 80 m; b) v = 40 m/s; 2. po složkách: 0 = m.ax, -mg = m.ay, ve vektorovém tvaru: (0, -mg) = m. (ax, ay)]
Maximum 3 body, průměr 2,09 bodů (69,8%), s = 0,28, 24 testů.
|
|
4
|
1.4.1999
čtvrtek 11,00'
doba:
13 minut
|
1. Je zadána rychlost jako funkce času v(t) = 12 t2 m/s. Spočítejte:
a) závislost zrychlení na čase, (1/2 bodu)
b) závislost uražené dráhy na čase. (1/2 bodu)
2. Přes nehmotnou kladku upevněnou na siloměru visí nehmotné lano, na jehož koncích jsou připevněna závaží o hmotnosti m1 = 1 kg a m2 = 2 kg.
a) Napište pohybovou rovnici. (1 bod)
b) Jakou sílu ukáže siloměr, nechají-li se závaží na kladce volně pohybovat?. (1 bod)
[1. a) a(t) = 24 t m/s; b) s(t) = 6 t3 + s0 m; 2. a) (m1 - m2)g = (m1 + m2)a ; b) F = 2T = 4g(m1m2)/(m1 + m2) = 80/3 N]
Maximum 3 body, průměr 1,95 bodů (64,9%), s = 0,64, 19 testů.
|
|
5
|
1.4.1999
čtvrtek 12,45'
doba:
8 minut
|
1. Je zadán vodorovný vrh tělesa v homogenním gravitačním poli nad zemským povrchem, odpor vzduchu zanedbejte. Osa x leží na zemském povrchu, osa y míří kolmo vzhůru, počáteční podmínky pak jsou dány jako r(0) = (0, h), v(0) = (v0, 0).
a) Za jak dlouho těleso dopadne na zemský povrch? (1 bod)
b) Jaká bude souřadnice x v místě dopadu? (1 bod)
Gravitační zrychlení uvažujte g = 10 m/s2.
2. Závaží o hmotnosti m1 klouzající s nulovým třením po vodorovné desce je spojeno lanem s druhým tělsem o hmotnosti m2, visícím přes kladku upevněnou na okraji desky.
S jakým zrychlením se bude soustava obou těles pohybovat?. (1 bod)
[1. a) t = 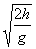 ; b) x = v0 ; b) x = v0 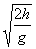 ; 2. a = (m2g / (m1 + m2)] ; 2. a = (m2g / (m1 + m2)]
Maximum 3 body, průměr 3,00 bodů (100,0%), s = 0,00, 24 testů.
|
|
6
|
1.4.1999
čtvrtek 14,30'
doba:
7 minut
|
1. Těleso vyhodíme kolmo vzhůru rychlostí v0= 10 m/s. Odpor vzduchu zanedbejte.
a) Napište závislost výšky tělaësa na čase. (1 bod)
b) Za jak dlouho se bude nacházet ve výšce h = 3,2 m nad zemským povrchem ? (1 bod)
Gravitační zrychlení uvažujte g = 10 m/s2.
2. Závaží o hmotnosti m1 klouzající s nulovým třením po vodorovné desce je spojeno lanem s druhým tělsem o hmotnosti m2, visícím přes kladku upevněnou na okraji desky.
Napište pohybovou rovnici soustavy obou těles. (1 bod)
[1. a) y(t) = -gt2/2 + v0t; b) t1 = 0,4 s; t2 = 1,6 s; 2. (m2g = (m1 + m2)a]
Maximum 3 body, průměr 2,57 bodů (85,5%), s = 0,60, 19 testů.
|
|
7
|
1.4.1999
čtvrtek 16,15'
doba:
10 minut
|
1. Z jaké výšky musíme pustit kámen, aby dopadl na zemský povrch za čas t = 6 s? (1 bod)
2. Přes pevnou kladku visí nehmotné lano, na jehož koncích jsou připevněna závaží o hmotnosti m1 a m2.
a) Napište pohybovou rovnici. (1 bod)
b) Jakou silou je napínáno lano? (1 bod)
[1. h = 180 m; 2. a) (m1 - m2)g = (m1 + m2)a; b) F = 2g (m1m2/(m1 + m2)]
Maximum 3 body, průměr 1,71 bodů (57,1%), s = 0,72, 14 testů.
|
|
8
|
2.4.1999
pátek 14,30'
doba:
20 minut
|
1. Zrychlení pohybujícího se tělesa rovnoměrně klesá tak, že na počátku je a(0) = 20 m/s2, v čase t1 je zrychlení a(t1) = 10 m/s2. Rychlost na počátku je v(0) = 1 m/s.
a) Jaké je zrychlení tělesa jako funkce času? (1 bod)
b) Jaká je rychlost tělesa v čase t1? (1 bod)
c) Jaká je celková uražená dráha tělesa v čase 0 < t < t1? (1 bod)
[1. a) a = t + 10 m/s2; b) v(t1) = 151 m/s; c) s = 5060/6 m]
Maximum 3 body, průměr 1,68 bodů (56,0%), s = 0,90, 18 testů.
|
|
9
|
2.4.1999
pátek 16,15'
doba:
10 minut
|
1. Těleso se pohybuje rovnoměrně zpomaleně, zastaví se během deseti sekund a urazí dráhu 100 m.
a) Jaké je zrychlení tělesa? (1 bod)
b) Jaká byla rychlost tělesa na počátku? (1 bod)
2. Závaží o hmotnosti m2 klouzající s nulovým třením po vodorovné desce je spojeno lanem s druhým tělsem o hmotnosti m1, visícím přes kladku upevněnou na okraji desky, na opačné straně je stejným spůsobem spojeno s tělesem o hmotnosti m3.
Napište pohybovou rovnici. (1 bod)
[1. a) a = -2 m/s2; b) v0 = 20 m/s; 2. (m1 + m2 + m3)a = (m1 - m3)g]
Maximum 3 body, průměr 2,88 bodů (96,2%), s = 0,30, 13 testů.
|
|
10
|
2.4.1999
pátek 18,00'
doba:
9 minut
|
1. Rychlost je dána funkcí v = 2e4t m/s.
a) Spočítejte závislost zrychlení na čase.(1 bod)
b) Spočítejte závislost dráhy na čase.(1 bod)
2. Přes pevnou nehmotnou kladku visí hmotné lano délky l a hmotnosti m. Hmotnost je rozložena rovnoměrně, obvod kladky je zanedbatelný vzhledem k délce lana. Napište pohybovou rovnici lana. (1 bod)
[1. a(t) = 8e4t m/s2; b) s(t) = 1/2 e4t + s0; 2. mg(2x - l)/l = ma]
Maximum 3 body, průměr 2,33 bodů (77,8%), s = 0,48, 12 testů.
|
|
11
|
13.4.1999
úterý 12,45'
doba:
11/2 minut
|
Na rovníku vyhodíme kamínek do výšky a necháme ho dopadnout zpět na zem. Kterým směrem se odchýlí bod dopadu v důsledku Coriolisovy síly?
Odpověď (1/2 bodu) , vysvětlení (1/2 bodu) .
[Odchýlí se na západ, kamínek si udržuje setrvačností obvodovou rychlost odpovídající zemskému povrchu na rovníku, aby byl stále nad stejným bodem zemského povrchu, musela by jeho obvodová rychlost růst, proto se za zemským povrchem spozdí.]
Maximum 1 bod, průměr 0,38 bodů (37,5%), s = 0,43, 16 testů.
Průměr dosažených bodů je velmi nízký, příklad stornován, body se nebudou počítat.
|
|
12
|
13.4.1999
úterý 12,45'
doba:
11/2 minut
|
Po půlkuhové rampě tvaru U necháme volně bez tření klouzat těleso o hmotnosti m = 1 kg z výšky R = 5 m s nulovou počáteční rychlostí. R je poloměr kruhového oblouku rampy.
a) Jakou rychlostí se těleso bude pohybovat v nejnižším bodě? (1 bod)
b) Jakou silou bude těleso působit na podložku v nejnižším bodě? (1 bod)
[a) v =10 m/s; b) F = 30 N]
Maximum 2 body, průměr 1,77 bodů (88,3%), s = 0,42, 16 testů.
|
|
13
|
13.4.1999
úterý 16,15'
doba:
15/2 minut
|
Automobil o hmotnosti m = 250 kg se pohybuje po rovné silnici, bez tření, vlastní sestrvačností stálou rychlostí v = 20 m/s. Přejede klenutý most, jehož převýšení je h = 12,2 m a poloměr kruhového oblouku mostu je R = 50 m.
a) Jakou rychlostí se automobil bude pohybovat v nejvyšším bodě mostu? (1 bod)
b) Jakou silou bude automobil působit na most v nejvyšším bodě? (1 bod)
Zanedbejte všechny ztráty třením a gravitační zrychlení uvažujte g = 10 m/s2.
[a) v2= 156 m/s; b) F= 17,7 N]
Maximum 2 body, průměr 1,16 bodů (58,2%), s = 0,55, 23 testů.
|
|
14
|
13.4.1999
úterý 16,15'
doba:
15/2 minut
|
Těleso o hmotnosti 1 kg klouže po vodorovném povrchu bez tření rychlostí v1 = 2 m/s, před ním klouže ve stejném směru těleso o hmotnosti 2 kg rychlostí v2 = 1 m/s. Ryhlejší těleso narazí do pomalejšího, dojde k nepružné srážce a obě tělesa splynou v jediné.
a) Jakou rychlostí se bude pohybovat výsledné těleso? (1 bod)
b) Jaká energie připadne na ztráty způsobené ohřátím těles, deformací ap? (1 bod)
[a) v = 4/3 m/s; b) Eztráty = 1/3 J]
Maximum 2 body, průměr 1,73 bodů (86,4%), s = 0,41, 23 testů.
|
|
15
|
13.4.1999
úterý 18,00'
doba:
10/2 minut
|
Po rovníku se pohybuje vlak ve směru na západ.Určete směr Coriolisovy síly (ze vzorce Fc = 2mvxw). (1 bod)
[Coriolisova síla bude směřovat do středu země]
Maximum 1 bod, průměr 0,82 bodů (81,8%), s = 0,36, 22 testů.
|
|
16
|
13.4.1999
úterý 18,00'
doba:
10/2 minut
|
Těleso o hmotnosti 1 kg klouže po vodorovném povrchu bez tření rychlostí v1 = 2 m/s, před ním klouže ve stejném směru těleso o hmotnosti 2 kg rychlostí v2 = 1 m/s. Ryhlejší těleso narazí do pomalejšího, dojde k nepružné srážce a obě tělesa splynou v jediné.
a) Jakou rychlostí se bude pohybovat výsledné těleso? (1 bod)
b) Jaká energie připadne na ztráty způsobené ohřátím těles, deformací ap? (1 bod)
[a) v = 4/3 m/s; b) Eztráty = 1/3 J]
Maximum 2 body, průměr 1,85 bodů (92,6%), s = 0,33, 22 testů.
|
|
17
|
15.4.1999
čtvrtek 11,00'
doba:
10/2 minut
|
Z břehu Antarktidy vyhodíme úlomek ledu směrem na sever tak, aby volně klouzal po zamrzlém povrchu. Jakým směrem se odchýlí od přímého směru v důsledku působení Coriolisovy síly? (1 bod)
[Odchýlí se vlevo, tj. na západ]
Maximum 1 bod, průměr 0,85 bodů (85,0%), s = 0,37, 20 testů.
|
|
18
|
15.4.1999
čtvrtek 11,00'
doba:
10/2 minut
|
Těleso o hmotnosti 1 kg klouže po vodorovném povrchu bez tření rychlostí v = 4 m/s, narazí do stojícího tělesa o hmotnosti 2 kg. Po nárazu bude mít první těleso rychlost opačně orientovanou o velikosti v1 = 1 m/s.
a) Jakou rychlostí v2 se bude pohybovat druhé těleso po srážce? (1 bod)
b) Jaká energie připadne na ztráty způsobené ohřátím těles, deformací ap? Půjde o dokonale pružnou srážku? Bude takto zadaná srážka možná? (1 bod)
[a) v = 5/2 m/s; b) Eztráty = 5/4 J]
Maximum 2 body, průměr 1,29 bodů (64,4%), s = 0,74, 20 testů.
|
|
19
|
15.4.1999
čtvrtek 12,45'
doba:
10/2 minut
|
Na severní polokouli země necháme padat kamínek volným pádem na zemský povrch.
a) Kterým směrem se odchýlí od svislého směru v důsledku Coriolisovy síly? (1/2 bodu)
b) Jak se změní odchylka, provedeme-li stejný experiment více na severu? (1/2 bodu) .
[Odchýlí se na východ, čím více na sever, tím bude odchylka menší]
Maximum 1 bod, průměr 0,60 bodů (60,4%), s = 0,47, 24 testů.
|
|
20
|
15.4.1999
čtvrtek 12,45'
doba:
10/2 minut
|
Automobil o hmotnosti m = 250 kg se pohybuje po rovné silnici, vlastní sestrvačností, stálou rychlostí v = 20 m/s. Přejede klenutý most, jehož převýšení je h = 7,2 m a poloměr kruhového oblouku mostu je R = 50 m.
a) Jakou rychlostí se automobil bude pohybovat v nejvyšším bodě mostu? (1 bod)
b) Jakou silou bude automobil působit na most v nejvyšším bodě? (1 bod)
Zanedbejte všechny ztráty třením a gravitační zrychlení uvažujte g = 10 m/s2.
[a) v = 16 m/s; b) F = 1220 N]
Maximum 2 body, průměr 1,67 bodů (83,3%), s = 0,58, 24 testů.
|
|
21
|
15.4.1999
čtvrtek 14,30'
doba:
15/2 minut
|
Z břehu Antarktidy vyhodíme úlomek ledu směrem na sever tak, aby volně klouzal po zamrzlém povrchu. Jakým směrem se odchýlí od přímého směru v důsledku působení Coriolisovy síly? (1 bod)
[Odchýlí se vlevo, tj. na západ]
Maximum 1 bod, průměr 0,68 bodů (67,6%), s = 0,47, 17 testů.
|
|
22
|
15.4.1999
čtvrtek 14,30'
doba:
15/2 minut
|
Po nakloněné rovině s úhlem sklonu 45o se pohybuje těleso s počáteční rychlostí v0 = 10 m/s směrem největšího stoupání. Koeficient tření mezi tělesem a rovinou je f = 0,2.
a) Jaké bude zrychlení tělesa? (1 bod)
b) Do jaké maximální výšky těleso vystoupí? (1 bod)
Gravitační zrychlení uvažujte g = 10 m/s2.
[a) a = g(1 + f)/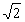 = 12/ = 12/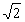 m/s2; b) h = v02/(2g(1 + f)) = 5/1,2 m] m/s2; b) h = v02/(2g(1 + f)) = 5/1,2 m]
Maximum 2 body, průměr 0,32 bodů (16,2%), s = 0,40, 17 testů.
Průměr dosažených bodů je velmi nízký, příklad stornován, body se nebudou počítat.
|
|
23
|
15.4.1999
čtvrtek 16,15'
doba:
10/2 minut
|
Po rovníku se pohybuje vlak ve směru na západ.Určete směr Coriolisovy síly (ze vzorce Fc = 2mvxw). (1 bod)
[Coriolisova síla bude směřovat do středu země]
Maximum 1 bod, průměr 0,59 bodů (58,9%), s = 0,50, 14 testů.
|
|
24
|
15.4.1999
čtvrtek 16,15'
doba:
10/2 minut
|
Těleso o hmotnosti 3 kg klouže po vodorovném povrchu bez tření rychlostí v = 4 m/s, narazí do stojícího tělesa o hmotnosti 4 kg. Po nárazu bude mít první těleso rychlost opačně orientovanou o velikosti v1 = 2 m/s.
a) Jakou rychlostí v2 se bude pohybovat druhé těleso po srážce? (1 bod)
b) Půjde o dokonale pružnou srážku? Bude takto zadaná srážka možná? (1 bod)
[v2 = 9/2 m/s; kinetická energie před srážkou je 24 J, energie po srážce je 93/2 J, srážka není možná; mohla by probíhat inverzně, tj. zaměníme-li hodnoty před a po srážce]
Maximum 2 body, průměr 1,30 bodů (65,2%), s = 0,75, 14 testů.
|
|
25
|
16.4.1999
pátek 14,30'
doba:
10/2 minut
|
Z břehu Antarktidy vyhodíme úlomek ledu směrem na sever tak, aby volně klouzal po zamrzlém povrchu. Jakým směrem se odchýlí od přímého směru v důsledku působení Coriolisovy síly? (1 bod)
[Odchýlí se vlevo, tj. na západ]
Maximum 1 bod, průměr 1,00 bodů (100,0%), s = 0,00, 20 testů.
|
|
26
|
16.4.1999
pátek 14,30'
doba:
10/2 minut
|
Těleso o hmotnosti 1 kg klouže po vodorovném povrchu bez tření rychlostí v = 4 m/s, narazí do stojícího tělesa o hmotnosti 2 kg. Po nárazu bude mít první těleso rychlost opačně orientovanou o velikosti v1 = 1 m/s.
a) Jakou rychlostí v2 se bude pohybovat druhé těleso po srážce? (1 bod)
b) Jaká energie připadne na ztráty způsobené ohřátím těles, deformací ap? Půjde o dokonale pružnou srážku? Bude takto zadaná srážka možná? (1 bod)
[a) v = 5/2 m/s; b) Eztráty = 5/4 J, srážka je možná, noboť ztráty vyšly nezáporné a je nepružná, neboť ztráty nejsou nulové]
Maximum 2 body, průměr 1,27 bodů (63,8%), s = 0,57, 20 testů.
|
|
27
|
16.4.1999
pátek 16,15'
doba:
10/2 minut
|
Na severní polokouli země necháme padat kamínek volným pádem na zemský povrch.
a) Kterým směrem se odchýlí od svislého směru v důsledku Coriolisovy síly? (1/2 bodu)
b) Jak se změní odchylka, provedeme-li stejný experiment více na severu? (1/2 bodu) .
[Odchýlí se na východ, čím více na sever, tím bude odchylka menší]
Maximum 1 bod, průměr 0,50 bodů (50,0%), s = 0,50, 13 testů.
|
|
28
|
16.4.1999
pátek 16,15'
doba:
10/2 minut
|
Po nakloněné rovině s úhlem sklonu 45o se pohybuje těleso s počáteční rychlostí v0 = 1 m/s směrem dolů. Jaká bude rychlost tělesa po uražení dráhy s = 5 m? (2 body)
Gravitační zrychlení uvažujte g = 10 m/s2.
[v = 8,47 m/s]
Maximum 2 body, průměr 1,69 bodů (84,6%), s = 0,48, 13 testů.
|
|
29
|
16.4.1999
pátek 18,00'
doba:
12/2 minut
|
Po půlkuhové rampě tvaru U necháme volně bez tření klouzat těleso o hmotnosti m = 1 kg z výšky R = 5 m s nulovou počáteční rychlostí. R je poloměr kruhového oblouku rampy.
a) Jakou rychlostí se těleso bude pohybovat v nejnižším bodě? (1 bod)
b) Jakou silou bude těleso působit na podložku v nejnižším bodě? (1 bod)
[a) v =10 m/s; b) F = 30 N]
Maximum 2 body, průměr 1,80 bodů (90,0%), s = 0,37, 15 testů.
|
|
30
|
16.4.1999
pátek 18,00'
doba:
12/2 minut
|
Těleso o hmotnosti 3 kg klouže po vodorovném povrchu bez tření rychlostí v = 1 m/s, narazí do stojícího tělesa o hmotnosti 4 kg. Po nárazu bude mít první těleso rychlost opačně orientovanou o velikosti v1 = 0,5 m/s.
a) Jakou rychlostí v2 se bude pohybovat druhé těleso po srážce? (1 bod)
b) Jaká energie připadne na ztráty způsobené ohřátím těles, deformací ap? Půjde o dokonale pružnou srážku? Bude takto zadaná srážka možná? (1 bod)
[a) v = 9/8 m/s; b) E = 9/8 J, E' = 93/32, Eztráty = -47/32 J, srážka není možná, neboť vychází záporná ztrátová energie; srážka by mohla probíhat inverzně, tj. jako když zaměníme hodnoty rychlostí těles před srážkou a po srážce, v tom případě by byla nepružná, neboť ztrátová energie je nenulová]
Maximum 2 body, průměr 1,45 bodů (72,5%), s = 0,45, 15 testů.
|
|
31
|
27.4.1999
úterý 12,45'
doba:
16/2 minut
|
Těleso o hmotnosti 1 kg leží na nakloněné rovině svírající s vodorovnou podložkou
= úhel 30°.
a) Nakreslete do obrázku všechny vnější síly působící na těleso (řešte jako pro hmotný bod). (1 bod)
b) Sestavte podmínky rovnováhy a vypočtěte pro jakou hodnotu koeficientu tření mezi
tělesem a podložkou se těleso udrží v klidu. (1 bod)
[a) jsou dvě síly, od podložky a od gravitačního pole, síla od podložky má kolmou
složku F a podélnou složku f.F; b) f = 1/tg(30°)]
Maximum 2 body, průměr 1,22 bodů (60,9%), s = 0,58, 16 testů.
|
|
32
|
27.4.1999
úterý 12,45'
doba:
16/2 minut
|
Jsou dány 3 hmotné body o hmotnostech m1 = m2 = 1 kg, m3
= 2 kg, jejichž polohové vektory jsou r1 = (0, 2, 4) m, r2
= (1, 1, 1) m a r3 = (4, 0, 0) m.
Spočítejte polohový vektor těžiště. (2 body)
[rT = (9, 3, 5)/4 m]
Maximum 2 body, průměr 1,69 bodů (84,4%), s = 0,70, 16 testů.
|
|
33
|
27.4.1999
úterý 16,15'
doba:
10/2 minut
|
Jsou dány 3 hmotné body o hmotnostech m1 = m2 = 1 kg, m3
= 2 kg, jejichž polohové vektory jsou r1 = (0, 2, 4) m, r2
= (1, 1, 1) m a r3 = (4, 0, 0) m.
Spočítejte polohový vektor těžiště. (2 body)
[rT = (9, 3, 5)/4 m]
Maximum 2 body, průměr 1,93 bodů (96,6%), s = 0,32, 22 testů.
|
|
34
|
27.4.1999
úterý 16,15'
doba:
10/2 minut
|
Homogenní koule má moment setrvačnosti vzhledem k ose procházející jejím středem
J = mR2, kde R je poloměr koule a R je její hmotnost.
a) Pomocí Steinerovy věty spočítejte moment setrvačnosti výstředně upevněné
koule pomocí ramene délky R. (1 bod)
b) Porovnejte moment setrvačnosti získaný podle bodu a) s momentem setrvačnosti pro případ,
nahradíme-li kouli hmotným bodem. (1 bod)
[a) J = 22 (mR2)/5; J2 = 4 mR2 < J]
Maximum 2 body, průměr 1,59 bodů (79,5%), s = 0,48, 22 testů.
|
|
35
|
27.4.1999
úterý 18,00'
doba:
10/2 minut
|
Homogenní tyč se otáčí kolem osy kolmé na tyč, vzdálenost bližšího konce od
osy je stejná jako délka tyče a je rovna l. Hmotnost tyče je m.
a) Integrací vypočítejte moment setrvačnosti tyče. (1 bod)
b) Vypočítejte tentýž moment setrvačnosti pomocí Steinerovy věty, víte-li, že
moment setrvačnosti vzhledem k ose procházející jejím středem J = ml2/12. (1 bod)
[a) J = 7 (ml2)/3]
Maximum 2 body, průměr 1,65 bodů (82,5%), s = 0,49, 20 testů.
|
|
36
|
27.4.1999
úterý 18,00'
doba:
10/2 minut
|
Jsou dány 3 hmotné body o hmotnostech m1 = m2 = 1 kg, m3
= 2 kg, jejichž polohové vektory jsou r1 = (0, 2, 4) m, r2
= (1, 1, 1) m a r3 = (4, 0, 0) m.
Spočítejte polohový vektor těžiště. (2 body)
[rT = (9, 3, 5)/4 m]
Maximum 2 body, průměr 1,88 bodů (93,8%), s = 0,46, 20 testů.
|
|
37
|
29.4.1999
čtvrtek 11,00'
doba:
15/2 minut
|
Homogenní tyč se otáčí kolem osy kolmé na tyč, vzdálenost bližšího konce od
osy je stejná jako délka tyče a je rovna l. Hmotnost tyče je m.
a) Integrací vypočítejte moment setrvačnosti tyče. (1 bod)
b) Vypočítejte tentýž moment setrvačnosti pomocí Steinerovy věty, víte-li, že
moment setrvačnosti vzhledem k ose procházející jejím středem J = ml2/12. (1 bod)
[a) J = 7 (ml2)/3]
Maximum 2 body, průměr 1,67 bodů (83,3%), s = 0,58, 21 testů.
|
|
38
|
29.4.1999
čtvrtek 11,00'
doba:
15/2 minut
|
Spočítejte souřadnici x těžiště velmi tenkého klínu délky l a hmotnosti m.
a) Určení délkové hustoty (1 bod)
b) Určení polohy těžiště integrací. (1 bod)
Nápověda: řešte jako velmi tenkou tyč, jejíž délková hustota se lineárně mění.
[a) t(x) = 2m/l2.x; b) Tx = 2/3.l. Pozn.: poloha těžiště
na ose x závisí jenom na rozložení hmoty podél osy x, stejný výsledek se tedy
dostane pro libovolně vysoký klínek, řešení je navíc možné získat z věty o těžnicích
v trojuhelníku]
Maximum 2 body, průměr 0,40 bodů (20,2%), s = 0,68, 21 testů.
Průměr dosažených bodů je velmi nízký, příklad stornován, body se nebudou počítat.
|
|
39
|
29.4.1999
čtvrtek 12,45'
doba:
22/2 minut
|
Nehomogenní nosník tvaru tyče, jehož délka je l a hmotnost m, má délkovou
hustotu jedné poloviny dvakrát větší než délkovou hustotu druhé poloviny. Nosník
položíme na dvě podpěry vzdálené o l, takže nosník bude podepřen v obou koncových
bodech.
a) Nakreslete do obrázku všechny vnější síly působící na nosník. (1/2 bodu)
b) Sestavte podmínky rovnováhy. (1 bod)
c) Řešením podmínek rovnováhy nalezněte reakční síly, jimiž působí podpěry na
nosník. (1/2 bodu)
[a) F1, F2 ... síly jimiž působí podpěry směrem nahoru,
2/3 mg a 1/3 mg, tíhy první a druhé poloviny nosníku působící v jedné a ve třech
čtvrtinách délky směrem dolů; b) F1 + F2 - mg = 0,
l/4.2/3 mg + 3l/4.1/3 mg - F2.l = 0; c) F1= 5/12 mg, F2
= 7/12 mg]
Maximum 2 body, průměr 1,55 bodů (77,3%), s = 0,49, 22 testů.
|
|
40
|
29.4.1999
čtvrtek 12,45'
doba:
22/2 minut
|
Velmi tenký klín z homogenního materiálu o délce l a hmotnosti m se otáčí kolem
osy kolmé na klín, klín je upevněn ve špičce.
a) Určete závislost délkové hustoty klínu na radiálním směru od osy. (1 bod)
b) Určete jeho moment setrvačnosti. (1 bod)
Nápověda: řešte jako moment setrvačnosti velmi tenké nehomogenní tyče, jejíž délková
hustota se mění lineárně.
[a) t(x) = 2m/l2.x; b) J = 1/2.ml2. Pozn.: Moment setrvačnosti
se nezmění, změníme-li rozložení hmoty v tělese při zachování radiálních vzdáleností,
klínek tedy můžeme z hlediska momentu setrvačnosti převést na válec, což souhlasí
se získaným výsledkem]
Maximum 2 body, průměr 0,20 bodů (10,2%), s = 0,53, 22 testů.
Průměr dosažených bodů je velmi nízký, příklad stornován, body se nebudou počítat.
|
|
41
|
29.4.1999
čtvrtek 14,30'
doba:
20/2 minut
|
Nehomogenní nosník tvaru tyče, jehož délka je l a hmotnost m, má délkovou
hustotu jedné poloviny dvakrát větší než délkovou hustotu druhé poloviny. Nosník
položíme na dvě podpěry vzdálené o l, takže nosník bude podepřen v obou koncových
bodech.
a) Nakreslete do obrázku všechny vnější síly působící na nosník. (1/2 bodu)
b) Sestavte podmínky rovnováhy. (1 bod)
c) Řešením podmínek rovnováhy nalezněte reakční síly, jimiž působí podpěry na
nosník. (1/2 bodu)
[a) F1, F2 ... síly jimiž působí podpěry směrem nahoru,
2/3 mg a 1/3 mg, tíhy první a druhé poloviny nosníku působící v jedné a ve třech
čtvrtinách délky směrem dolů; b) F1 + F2 - mg = 0,
l/4.2/3 mg + 3l/4.1/3 mg - F2.l = 0; c) F1= 5/12 mg, F2
= 7/12 mg]
Maximum 2 body, průměr 1,20 bodů (60,0%), s = 0,55, 20 testů.
|
|
42
|
29.4.1999
čtvrtek 14,30'
doba:
20/2 minut
|
Spočítejte souřadnici x těžiště velmi tenkého klínu délky l a hmotnosti m.
a) Určení délkové hustoty (1 bod)
b) Určení polohy těžiště integrací. (1 bod)
Nápověda: řešte jako velmi tenkou tyč, jejíž délková hustota se lineárně mění.
[a) t(x) = 2m/l2.x; b) Tx = 2/3.l. Pozn.: poloha těžiště
na ose x závisí jenom na rozložení hmoty podél osy x, stejný výsledek se tedy
dostane pro libovolně vysoký klínek, řešení je navíc možné získat z věty o těžnicích
v trojuhelníku]
Maximum 2 body, průměr 0,23 bodů (11,3%), s = 0,41, 20 testů.
Průměr dosažených bodů je velmi nízký, příklad stornován, body se nebudou počítat.
|
|
43
|
29.4.1999
čtvrtek 16,15'
doba:
14/2 minut
|
Těleso o hmotnosti 1 kg leží na nakloněné rovině svírající s vodorovnou podložkou
= úhel 30°.
a) Nakreslete do obrázku všechny vnější síly působící na těleso (řešte jako pro hmotný bod). (1 bod)
b) Sestavte podmínky rovnováhy a vypočtěte pro jakou hodnotu koeficientu tření mezi
tělesem a podložkou se těleso udrží v klidu. (1 bod)
[a) jsou dvě síly, od podložky a od gravitačního pole, síla od podložky má kolmou
složku F a podélnou složku f.F; b) f = 1/tg(30°)]
Maximum 2 body, průměr 1,03 bodů (51,5%), s = 0,80, 17 testů.
|
|
44
|
29.4.1999
čtvrtek 16,15'
doba:
14/2 minut
|
V bodě určeném polohovým vektorem r = (1, 4, 2) m působí síla F
= (-2, 0, 2) N.
Určete moment síly vzhledem k počátku. (2 body)
[M = (8, -6, 8) Nm]
Maximum 2 body, průměr 1,18 bodů (58,8%), s = 0,39, 17 testů.
|
|
45
|
18.5.1999
úterý 12,45'
doba:
20/2 minut
|
Délka tyče při natahování silou F1 = 10 N je l1 = 1,1 m, při
síle F2 = 50 N je délka tyče l2 = 1,2 m.
a) Napište soustavu rovnic pro vztahy mezi délkami a silami. (1
bod)
b) Řešte tuto soustavu a vypočítejte klidovou délku l a Youngův modul pružnosti E. (1 bod)
[l = (l1F2 - l2F1)/(F2 - F1)
= (55 - 12)/40 = 1,075 m; E = (l1F2 - l2F1)/S(l2
- l1) = 104.(55 - 12)/0,1 = 4,3.106 N/m2]
Maximum 2 body, průměr 1,42 bodů (70,8%), s = 0,73, 12 testů.
|
|
46
|
18.5.1999
úterý 12,45'
doba:
20/2 minut
|
Na přímce se nacházejí dva bodové náboje q1 = 1 C a q2 = 2
C. Vzdálenost nábojů je r = 20 m.
a) Jaká je intenzita elektrického pole E uprostřed mezi náboji? (2 body)
V řešení použijte konstantu K = 1/4pe0.
[E = E1 + E2 = K/100 (q1 - q2) = -K/100 V/m]
Maximum 2 body, průměr 1,83 bodů (91,7%), s = 0,39, 12 testů.
|
|
47
|
18.5.1999
úterý 16,15'
doba:
20/2 minut
|
Na přímce se nacházejí dva bodové náboje q1 = 1 C a q2 = 2
C. Vzdálenost nábojů je r = 20 m.
a) Jaká je intenzita elektrického pole E uprostřed mezi náboji? (2 body)
V řešení použijte konstantu K = 1/4pe0.
[E = E1 + E2 = K/100 (q1 - q2) = -K/100 V/m]
Maximum 2 body, průměr 1,55 bodů (77,3%), s = 0,67, 22 testů.
|
|
48
|
18.5.1999
úterý 16,15'
doba:
20/2 minut
|
Vodorovná trubice o různých průřezech je protékána vodou. V místě průřezu S1
= 30 cm2 je rychlost vody v1 = 5 m/s a tlak P1 = 2.105
Pa. Tlak v jiném místě trubice je P2 = 1.105 Pa.
a) Spočítejte rychlost v2. (1 bod)
b) Spočítejte průřez trubice S2. (1 bod)
V řešení použijte hustotu vody r = 1000 kg/m3.
[v2 = 15 m/s; S2 = 10 cm2]
Maximum 2 body, průměr 1,70 bodů (85,2%), s = 0,67, 22 testů.
|
|
49
|
18.5.1999
úterý 18,00'
doba:
20/2 minut
|
Hmotný bod o hmotnosti 1 kg se nachází ve vzdálenosti 200 milionů km od slunce a leží na stejné
přímce jako slunce a země, země je mezi hmotným bodem a sluncem ve vzdálenosti 150
milionů km od slunce.
a) Spočítejte celkovou gravitační sílu, jíž působí na těleso země i slunce
dohromady. (2 body)
Hmotnost slunce je M = 2.1030 kg, hmotnost země je m = 6.1024 kg,
gravitační konstanta je G = 6,67.10-11
m3/kg.s2.
[F = 3,3.10-3 N, dominuje síla od slunce, síla od Země vychází asi o 4 řády menší.]
Maximum 2 body, průměr 1,88 bodů (94,1%), s = 0,49, 17 testů.
|
|
50
|
18.5.1999
úterý 18,00'
doba:
20/2 minut
|
Vodorovná trubice o různých průřezech je protékána vodou. V místě průřezu S1
= 30 cm2 je rychlost vody v1 = 5 m/s a tlak P1 = 2.105
Pa. Tlak v jiném místě trubice je P2 = 1.105 Pa.
a) Spočítejte rychlost v2. (1 bod)
b) Spočítejte průřez trubice S2. (1 bod)
V řešení použijte hustotu vody r = 1000 kg/m3.
[v2 = 15 m/s; S2 = 10 cm2]
Maximum 2 body, průměr 1,94 bodů (97,1%), s = 0,24, 17 testů.
|
|
51
|
20.5.1999
čtvrtek 11,00'
doba:
15/2 minut
|
Délka tyče o průřezu S = 1 cm2 při natahování silou F = 100 N je l1 = 1,26 m. Youngův modul pružnosti je E = 2.107 A/m3.
a) Vypočítejte klidovou délku tyče l0. (1
bod)
b) Určete relativní deformaci e. (1 bod)
[l0 = 1,2 m; e = 0,05]
Maximum 2 body, průměr 1,95 bodů (97,4%), s = 0,23, 19 testů.
|
|
52
|
20.5.1999
čtvrtek 11,00'
doba:
15/2 minut
|
Vodorovná trubice naplněná vodou je z jedné strany uzavřena pístem o ploše S = 10 cm2, z druhé strany je k trubici připojena tryska mířící směrem vzhůru. Do jaké výšky vystoupí voda, budeme-li na píst tlačit silou F = 20000 N ? (2 body)
V řešení použijte hustotu vody r = 1000 kg/m3 a gravitační konstantu g = 10 m/s2.
[hmax = 2000 m]
Maximum 2 body, průměr 1,74 bodů (86,8%), s = 0,63, 19 testů.
|
|
53
|
20.5.1999
čtvrtek 12,45'
doba:
15/2 minut
|
Vodorovná trubice naplněná vodou je z jedné strany uzavřena pístem o ploše S = 10 cm2, z druhé strany je k trubici připojena tryska mířící směrem vzhůru. Síla působící na píst je F = 200 N, atmosférický tlak neuvažujte.
a) Vypočítejte rychlost vody vytékající z trysky. (1
bod)
b) Do jaké výšky dostříkne voda? (1 bod)
V řešení použijte hustotu vody r = 1000 kg/m3 a gravitační konstantu g = 10 m/s2.
[v = 20 m/s; hmax = 20 m]
Maximum 2 body, průměr 1,86 bodů (93,2%), s = 0,47, 22 testů.
|
|
54
|
20.5.1999
čtvrtek 12,45'
doba:
15/2 minut
|
Družice obíhá ve vzdálenosti R od zemského povrchu, kde R je rovno poloměru země, R = 6,4.106 m. Spočítejte rychlost družice.(2 body)
[v = 5,66 km/s]
Maximum 2 body, průměr 1,73 bodů (86,4%), s = 0,55, 22 testů.
|
|
55
|
20.5.1999
čtvrtek 14,30'
doba:
15/2 minut
|
Na přímce se nacházejí dva bodové náboje q1 = 1 C a q2 = 2
C. Vzdálenost nábojů je r = 20 m.
a) Jaká je intenzita elektrického pole E uprostřed mezi náboji? (2 body)
V řešení použijte konstantu K = 1/4pe0.
[E = E1 + E2 = K/100 (q1 - q2) = -K/100 V/m]
Maximum 2 body, průměr 1,94 bodů (96,9%), s = 0,25, 16 testů.
|
|
56
|
20.5.1999
čtvrtek 14,30'
doba:
15/2 minut
|
Hmotný bod o hmotnosti 1 kg se nachází ve vzdálenosti 200 milionů km od slunce a leží na stejné
přímce jako slunce a země, země je mezi hmotným bodem a sluncem ve vzdálenosti 150
milionů km od slunce.
a) Spočítejte celkovou gravitační sílu, jíž působí na těleso země i slunce
dohromady. (2 body)
Hmotnost slunce je M = 2.1030 kg, hmotnost země je m = 6.1024 kg,
gravitační konstanta je G = 6,67.10-11
m3/kg.s2.
[F = 3,3.10-3 N, dominuje síla od slunce, síla od Země vychází asi o 4 řády menší.]
Maximum 2 body, průměr 1,67 bodů (83,3%), s = 0,36, 15 testů.
|
|
57
|
21.5.1999
pátek 14,30'
doba:
15/2 minut
|
Vodorovná trubice o různých průřezech je protékána vodou. V místě průřezu S1
= 30 cm2 je rychlost vody v1 = 5 m/s a tlak P1 = 2.105
Pa. Tlak v jiném místě trubice je P2 = 1.105 Pa.
a) Spočítejte rychlost v2. (1 bod)
b) Spočítejte průřez trubice S2. (1 bod)
V řešení použijte hustotu vody r = 1000 kg/m3.
[v2 = 15 m/s; S2 = 10 cm2]
Maximum 2 body, průměr 2,11 bodů (105,3%), s = 0,46, 19 testů.
|
|
58
|
21.5.1999
pátek 14,30'
doba:
15/2 minut
|
V bodě určeném polohovým vektorem r = (1, 4, 2) m působí síla F
= (-1, 2, 0) N.
Určete moment síly vzhledem k bodu (1, 0, 0) m. (2 body)
[M = (2, 2, 4) Nm]
Maximum 2 body, průměr 1,76 bodů (88,2%), s = 0,26, 19 testů.
|
|
59
|
21.5.1999
pátek 16,15'
doba:
15/2 minut
|
Délka o průřezu S = 1 cm2 tyče při natahování silou F = 100 N je l1 = 1,26 m. Youngův modul pružnosti je E = 2.107 A/m3.
a) Vypočítejte klidovou délku tyče l0. (1
bod)
b) Určete relativní deformaci e. (1 bod)
[l0 = 1,2 m; e = 0,05]
Maximum 2 body, průměr 1,91 bodů (95,5%), s = 0,20, 11 testů.
|
|
60
|
21.5.1999
pátek 16,15'
doba:
15/2 minut
|
V bodě určeném polohovým vektorem r = (1, 4, 2) m působí síla F
= (1, 2, 0) N.
Určete moment síly vzhledem k bodu (1, 0, 0) m. (2 body)
[M = (-4, 2, -4) Nm]
Maximum 2 body, průměr 1,50 bodů (75,0%), s = 0,77, 11 testů.
|
|
61
|
21.5.1999
pátek 18,00'
doba:
15/2 minut
|
V bodě určeném polohovým vektorem r = (3, -1, 0) m působí síla F
= (3, 1, -1) N.
Určete moment síly vzhledem k bodu (2, 0, 0) m. (2 body)
[M = (1, 1, 4) Nm]
Maximum 2 body, průměr 1,72 bodů (85,9%), s = 0,31, 16 testů.
|
|
62
|
21.5.1999
pátek 18,00'
doba:
15/2 minut
|
Vodorovná trubice naplněná vodou je z jedné strany uzavřena pístem o ploše S = 10 cm2, z druhé strany je k trubici připojena tryska mířící směrem vzhůru. Síla působící na píst je F = 200 N, atmosférický tlak neuvažujte.
a) Vypočítejte rychlost vody vytékající z trysky. (1
bod)
b) Do jaké výšky dostříkne voda? (1 bod)
V řešení použijte hustotu vody r = 1000 kg/m3 a gravitační konstantu g = 10 m/s2.
[v = 20 m/s; hmax = 20 m]
Maximum 2 body, průměr 1,88 bodů (93,8%), s = 0,22, 16 testů.
|
|
63
|
27.5.1999
čtvrtek 16,15'
doba:
15/2 minut
|
Délka tyče o průřezu S = 1 cm2 při natahování silou F = 100 N je l1 = 1,26 m. Youngův modul pružnosti je E = 2.107 A/m3.
a) Vypočítejte klidovou délku tyče l0. (1
bod)
b) Určete relativní deformaci e. (1 bod)
[l0 = 1,2 m; e = 0,05]
Maximum 2 body, průměr 2,00 bodů (100,0%), s = 0,00, 15 testů.
|
|
64
|
27.5.1999
čtvrtek 16,15'
doba:
15/2 minut
|
Vodorovná trubice naplněná vodou je z jedné strany uzavřena pístem o ploše S = 10 cm2, z druhé strany je k trubici připojena tryska mířící směrem vzhůru. Síla působící na píst je F = 200 N, atmosférický tlak neuvažujte.
a) Vypočítejte rychlost vody vytékající z trysky. (1
bod)
b) Do jaké výšky dostříkne voda? (1 bod)
V řešení použijte hustotu vody r = 1000 kg/m3 a gravitační konstantu g = 10 m/s2.
[v = 20 m/s; hmax = 20 m]
Maximum 2 body, průměr 2,00 bodů (100,0%), s = 0,00, 15 testů.
|