| |
Kvantová kryptografie
Vojtěch Hála, 4. dubna 2005
Potřeba utajovat komunikaci je stará jako lidská civilizace. Po staletí vymýšleli
kryptografovéKryptografie
– věda zabývající se utajováním smyslu zpráv převodem do podoby, která
je čitelná jen se speciální znalostí. Slovo pochází z řečtiny: kryptós je skrytý a gráphein
znamená psát. Někdy je pojem obecněji používán pro vědu o čemkoli
spojeném se šiframi a je alternativou k pojmu kryptologie.
stále složitější šifryŠifra
– způsob změny tajné zprávy, aby její smysl mohl zjistit jen oprávněný
adresát. Někdy se slovo šifra používá pro samu zašifrovanou zprávu. a kryptoanalyticiKryptoanalýza – věda zabývající se metodami zjištění původní informace ze zašifrované bez znalosti klíče. Slovo pochází z řečtiny: kryptós je skrytý a analýein znamená rozvázat, uvolnit.
je s různou úspěšností luštili. V různých etapách tohoto
závodu měli navrch jedni či druzí a zdálo se, že boj je svou podstatou nekonečný. Může snad
existovat absolutně bezpečná šifra? Jedna taková byla již dávno nalezena, avšak brzy se ukázalo,
že v praxi je možné ji používat jen velmi omezeně. Překvapivou revoluci do těchto otázek přinesla
moderní fyzika. Kvantová kryptografie nabízí nepodmíněnou bezpečnostNepodmíněná bezpečnost
– znamená vysokou bezpečnost utajení, která není podmíněna žádnými
předpoklady na schopnosti a technické možnosti útočníka. Takovou
míru bezpečnosti dnes nabízí kvantová kryptografie a Vernamova
šifra., to znamená absolutní utajení
zaručené přírodními zákony. Je možné, že závod bude jednou pro vždy rozhodnut ve prospěch kryptografů?
|
Kryptografie
– věda zabývající se utajováním smyslu zpráv převodem do podoby, která
je čitelná jen se speciální znalostí. Slovo pochází z řečtiny: kryptós je skrytý a gráphein
znamená psát. Někdy je pojem obecněji používán pro vědu o čemkoli
spojeném se šiframi a je alternativou k pojmu kryptologie.
Kryptoanalýza – věda zabývající se metodami zjištění původní informace ze zašifrované bez znalosti klíče. Slovo pochází z řečtiny: kryptós je skrytý a analýein znamená rozvázat, uvolnit.
Kryptologie – věda o utajování zpráv ve všech formách zahrnující kryptografii a kryptoanalýzu. Slovo pochází z řečtiny: kryptós je skrytý a logos znamená původně slovo, v přeneseném smyslu vědění.
Nepodmíněná bezpečnost – znamená vysokou bezpečnost utajení,
která není podmíněna žádnými předpoklady na schopnosti a technické
možnosti útočníka. Takovou míru bezpečnosti dnes nabízí kvantová
kryptografie a Vernamova šifra.
Alice a Bob – tradiční jména pro komunikující osoby užívaná
v kryptografii. Jména parně vznikla zpříjemněním označení osob A
a B. Někdy se k nim přidává Eva (eavesdropper), která se snaží narušit bezpečnost komunikace.
GM počítač – Geigerův-Müllerův počítač. Jde o detektor
ionizujícího záření. Plyn v detekční trubici změní po vniknutí
částice svou vodivost. Detektor je citlivý na energetické fotony, alfa
částice a elektrony. Není citlivý k neutronům.
Radioaktivita – přeměna jader nestabilních nuklidů na jiná
jádra, při níž vzniká ionizující záření. Pokud se změní v jádře
počet protonů, dojde ke změně prvku. Rychlost přeměny je
charakterizována poločasem rozpadu. Radioaktivitu objevil v roce
1896 Henri Becquerel u solí uranu.
|
Vernamova šifra
V roce 1917 si Gilbert
Vernam dal patentovat vylepšení dřívějších způsobů šifrování. Vezmeme jednotlivá
písmena tajné zprávy a každé z nich posuneme o několik pozic v abecedě. Například první písmeno je
posunuto o 5 pozic, druhé o 1, třetí o 14, čtvrté o 24, další o 9, 0, 3, 9, 19. Když při posouvání
překročíme konec abecedy, pokračujeme od jejího začátku. Ze slova ALDEBARAN tak dostaneme šifrovaný
text FMRCKAUJG. Posloupnost 5, 1, 14, 24, 9, 0, 3, 9, 19 je klíčem k rozluštění zprávy. Kdo ji zná, dokáže
snadno posunout písmena opačným směrem a získat původní text. Bez znalosti klíče je luštění odposlechnuté
zprávy krajně obtížné, i když útočník ví, o jakou šifru jde. Aby byla Vernamova šifra spolehlivá, je
nutno dodržet tři požadavky:
- Klíč je stejně dlouhý jako přenášená zpráva. (Ve starších šifrách to bylo jinak.)
- Klíč je dokonale náhodný. (Generátory pseudonáhodných čísel nepřipadají v úvahu, nejlepší je užití
fyzikálních metod.)
-
Klíč nelze použít opakovaně. (Žádné dvě zprávy nesmí být šifrovány stejným klíčem.)
Porušení libovolného z těchto pravidel umožní útočníkovi odhalit tajný text, postupy jsou známé. Naopak
když požadavkům vyhovíme, můžeme si být bezpečností svých dat velmi jisti. Ani útok tzv. hrubou silou,
neboli zkoušení všech možných klíčů, nepomůže. Jeho výsledkem budou všechny možné zprávy dané délky,
mezi nimiž nepoznáme, která byla odesílána. Lze matematicky dokázat, že bez znalosti klíče nelze
zašifrovanou zprávu rozeznat od náhodné posloupnosti písmen. Co víc si přát! Vernamova šifra, anglicky
nazývaná one-time-pad, je dosud jedinou šifrou, jejíž neprolomitelnost byla exaktně dokázána (1949,
C. E. Shannon).
Popsané zacházení s klíčem je ale v praxi velice obtížné. Dlouhý náhodný klíč si člověk nedokáže
zapamatovat, musí být zaznamenán. Jeho generování není jednoduché. Musí být zajištěno, že klíč zná pouze
odesilatel a příjemce zprávy a nikdo jiný. Komunikující strany se tedy musí předem dohodnout na dlouhém
klíči nějakým bezpečným způsobem a hned po odeslání první zprávy klíč zničit. Stojíme tak před problémem
slepice a vejce: Abychom mohli bezpečně odeslat třeba 2 MB tajných dat, musíme předem bezpečně odeslat
2 MB dat (klíč). Vernamova šifra se tak i přes svou sílu používala jen výjimečně.
Dodejme, že Vernamova šifra funguje beze změn nad jakoukoliv množinou znaků, například jen 0 a 1. Posun
písmen nad dvouznakovou abecedou je možný pouze o 1 místo nebo 0 míst, klíčem je tedy také posloupnost
0 a 1. Každý bitbit – základní jednotka informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda), atd. klíče odpovídá jednomu bitu
zprávy a říká, zda se tento bitbit – základní jednotka informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda), atd. má při šifrování změnit
nebo nechat. Tato operace se dvěma bity se jmenuje XOR a značíme ji
 . .
| x |
y |
x y y |
(x y) y) y = x
y = x |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
K dešifrování stačí vzít šifrovaný text a provést XOR znovu se stejným klíčem, což se projeví jako
posun písmen opačným směrem.
Důsledky kvantové mechaniky
Může kvantová mechanika usnadnit správné zacházení s klíčem? První zajímavá vlastnost kvantového světa
je, že obsahuje náhodnost. Nabízí velké množství možností jak získat dokonale náhodný klíč. Například vezmeme
vzorek látky podléhající radioaktivnímu rozpaduRadioaktivita
– přeměna jader nestabilních nuklidů na jiná jádra, při níž vzniká
ionizující záření. Pokud se změní v jádře počet protonů, dojde ke
změně prvku. Rychlost přeměny je charakterizována poločasem rozpadu.
Radioaktivitu objevil v roce 1896 Henri Becquerel u solí
uranu.
a Geiger-Müllerův počítačGM počítač
– Geigerův-Müllerův počítač. Jde o detektor ionizujícího záření.
Plyn v detekční trubici změní po vniknutí částice svou vodivost.
Detektor je citlivý na energetické fotony, alfa částice
a elektrony. Není citlivý k neutronům. a měříme
velmi přesně čas mezi rozpady jader.
Posledních několik číslic časového údaje lze považovat za zcela náhodná čísla. Máme tedy bezedný zdroj
náhodných dat pro klíč. Jak je ale utajeně dostat od odesilatele k příjemci?
Další specialita kvantové mechaniky umožňuje vyřešit i tento problém. Provedeme-li na kvantovém systému
měření, nevyhnutelně tím systém ovlivníme. Komunikující strany by toho mohly využít k rozpoznání, zda je
někdo odposlouchává. V roce 1984 navrhli
Charles Bennett a Gilles Brassard kryptografický protokol postavený
na kvantové mechanice. Podle počátečních písmen objevitelů a podle roku objevu se protokol označuje BB84.
K přenosu informací se používají současně dvě přenosové cesty, dva
kanály. Jeden je klasický, například
telefon nebo Internet. Odposlouchávání na tomto kanále neprozradí nic
tajného, půjde přes něj zašifrovaná zpráva
a několik vedlejších informací. Druhý kanál je kvantový
a slouží k domluvení tajného klíče. K přenosu informace
využívá fotonů s různou polarizacíPolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi..
Možné jsou 4 roviny polarizací fotonuPolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi.,
dvě z nich reprezentují jedničkový
bitbit – základní jednotka informace, která nabývá dvou hodnot (ano/ne), (0/1), (pravda/nepravda), atd., druhé dvě nulový.
| Polarizační stav | Bitová hodnota | Báze |
|---|
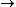 |
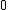 |
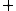 |
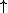 |
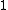 |
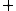 |
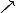 |
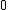 |
 |
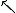 |
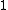 |
 |
Reprezentace bitů pomocí fotonů polarizovaných ve 4 rovinách.
|
K testování polarizace slouží měření ve dvou různých bázích, označíme
je
 a a
 . .
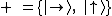
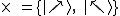
V báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze.  může
být výsledkem měření polarizace může
být výsledkem měření polarizace 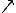 nebo nebo 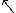 .
V báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze. .
V báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze.
 můžeme dostat výsledek můžeme dostat výsledek 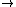 nebo nebo 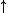 . Z kvantové mechaniky plyne, že pokud
zvolíme správnou báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze., výsledek měření bude odpovídat
polarizaci fotonuPolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi.. Pokud zvolíme nesprávnou báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze.,
dostaneme jeden z možných výsledků zcela náhodně s pravděpodobností
0,5.
Polarizace fotonuPolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi. se přitom
zákonitě změní na tu, která byla výsledkem měření, takže není možno měřit v obou bázích současně
a získat tak plnou informaci o stavu fotonu. Proč je to tak? . Z kvantové mechaniky plyne, že pokud
zvolíme správnou báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze., výsledek měření bude odpovídat
polarizaci fotonuPolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi.. Pokud zvolíme nesprávnou báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze.,
dostaneme jeden z možných výsledků zcela náhodně s pravděpodobností
0,5.
Polarizace fotonuPolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi. se přitom
zákonitě změní na tu, která byla výsledkem měření, takže není možno měřit v obou bázích současně
a získat tak plnou informaci o stavu fotonu. Proč je to tak?
Měření v bázi + ovlivňuje kvantový stav fotonu jako operátor vyjádřený
hermitovskou maticíHermitovská matice
– matice nad komplexními čísly, jejíž diagonálně sdružené prvky jsou
komplexně sdružené. Taková matice má všechna vlastní čísla reálná
a vlastní vektory navzájem kolmé. V kvantové mechanice se
hermitovské matice používají jako operátory pozorovatelné veličiny
a jejich vlastní čísla odpovídají naměřeným hodnotám., označme ji A
a definujme
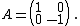
Vlastní hodnoty +1 a −1 odpovídají pozorování fotonů v jedné a druhé
polarizaciPolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi..
Příslušné
vlastní vektoryVlastní vektor – Vektor, který je operátorem jen komplexně natahován. (1, 0) a (0, 1) odpovídají polarizačním stavům
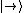 a
a 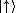 .
Vektory z druhé báze vyjádříme takto: .
Vektory z druhé báze vyjádříme takto:
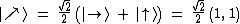
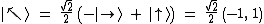
Měříme-li operátorem A některý z vlastních stavůVlastní stav – stav, který je vlastním vektorem příslušného operátoru. matice A, je stav pouze vynásoben reálným číslem a fyzikálně
se nezmění. Změříme-li na témže stavu jinou veličinu vyjádřenou operátorem B, bude výsledkem náhodně jeden
z vlastních stavůVlastní stav – stav, který je vlastním vektorem příslušného operátoru. matice B. Pravděpodobnost naměření stavu
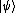 ,
když je foton například ve stavu ,
když je foton například ve stavu
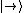 ,
spočteme jako kvadrát velikosti
skalárního součinuSkalární součin
– funkce, která dvojici prvků Hilbertova prostoru přiřazuje komplexní
číslo. V kvantové mechanice zapisujeme skalární součin Φ a Ψ jako
<Φ|Ψ>. Druhá mocnina jeho absolutní hodnoty vyjadřuje
pravděpodobnost, že při měření systému ve stavu Ψ zjistíme stav Φ. ,
spočteme jako kvadrát velikosti
skalárního součinuSkalární součin
– funkce, která dvojici prvků Hilbertova prostoru přiřazuje komplexní
číslo. V kvantové mechanice zapisujeme skalární součin Φ a Ψ jako
<Φ|Ψ>. Druhá mocnina jeho absolutní hodnoty vyjadřuje
pravděpodobnost, že při měření systému ve stavu Ψ zjistíme stav Φ. 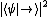 . Výpočtem dostaneme: . Výpočtem dostaneme:
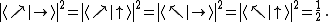
Z toho vidíme, že měřením v nesprávné báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze. dostaneme zcela náhodný výsledek.
Navíc foton přejde do vlastního stavuVlastní stav – stav, který je vlastním vektorem příslušného operátoru. nesprávné bázeBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze., a tím je ztracena veškerá informace, kterou nesl. Nešlo by nějak měřit v obou bázích současně?
Tomu by odpovídal operátor vyjádřený maticovým součinem AB, kde B je měření v bázi
 . Je to ale možné jen
pro nezávislé veličiny, tedy pokud AB = BA. Jak vypadá matice B? Odpovídá matici A po přechodu ke druhé báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze., tedy
násobené maticí otočení o +π/4. . Je to ale možné jen
pro nezávislé veličiny, tedy pokud AB = BA. Jak vypadá matice B? Odpovídá matici A po přechodu ke druhé báziBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze., tedy
násobené maticí otočení o +π/4.
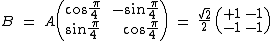
Známe matice obou operátorů, můžeme vypočítat komutátorKomutátor
– operace, která vyjadřuje, nakolik dvě jiné matice komutují. Značí se
[A, B] a vypočte se jako AB−BA. Je-li násobení matic A
a B komutativní, vyjde nulová matice. V kvantové mechanice je
možné měřit současně jen veličiny, jejichž operátory komutují. Je-li
komutátor nenulový, platí relace neurčitosti. [A, B].
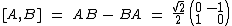 . .
Pro kompatibilní veličiny by musela vyjít nulová matice. Vidíme, že nelze měřit
v obou bázíchBáze
– maximální množina lineárně nezávislých vektorů v lineárním
vektorovém prostoru. Každý prvek prostoru lze jednoznačným způsobem
napsat jako lineární kombinaci prvků baze. zároveň.
Musíme provést dvě měření a zvolit jejich pořadí. Stav fotonu se přitom dvakrát změní.
|
BB84 - Kvantový protokol výměny klíče
Pro osoby vystupující v šifrovacím protokolu se tradičně užívají jména Alice, Bob
a Eva. Bob a Alice se chtějí dohodnout na tajném klíči, Eva chce klíč
nepozorovaně zjistit.
-
Alice generuje fotony polarizované náhodně s rovnoměrným rozložením mezi 4 možné roviny. Odesílá je
kvantovým kanálem Bobovi. Počet odeslaných fotonů musí přesahovat dvojnásobek počtu bitů tajné zprávy.
-
Bob provádí na fotonech měření, přičemž náhodně střídá báze. Zaznamenává si výsledky měření.
-
Alice sdělí Bobovi veřejným kanálem pořadí bází, v nichž byly jednotlivé fotony polarizovány. Konkrétní
hodnoty polarizace si ovšem nechá pro sebe.
-
Bob si poznamená hodnoty polarizací pro fotony, které měřil ve správné bázi. Tyto bity budou tvořit klíč.
Ostatní výsledky měření mohou být zapomenuty (zhruba polovina všech měření).
-
Bob veřejně sdělí Alici, které fotony měřil ve správné bázi. Alice ví, s jakou polarizací tyto fotony
posílala, takže zná všechny bity klíče. Bob je správně měřil, a tedy rovněž zná klíč. Zbývá poslední krok.
-
Několik náhodně zvolených bitů klíče musí být „obětováno“. Alice a Bob si je navzájem veřejně sdělí
a porovnají svoje hodnoty. Pokud se shodují, je všechno v pořádku a ostatní bity klíče budou použity pro
Vernamovu šifru. Pokud se některé bity neshodují, znamená to, že linka je odposlouchávána. V tom
případě musí být celý klíč zapomenut a postup zopakován od začátku.
Eva má jedinou možnost, jak získat tajný klíč – odposlouchávat kvantový komunikační kanál, neboli
provádět měření na Aliciných fotonech. Bude měřit ve stejných dvou bázích jako Bob, protože jedině tak
může z fotonů dekódovat potřebné bity klíče. Nemá ale šanci změřit jeden foton v obou bázích zároveň, jde
o nekomutující operátory. Pokud Eva zvolí správnou bázi, dostane správný výsledek, stav fotonu se nezmění
a nikdo nic nepozná. Pokud ale změří některý foton v nesprávné bázi, změní se jeho kvantový stav a výsledek
Bobova správného měření pak bude náhodný. V 50 % těchto případů se ani tak nic neodhalí, protože Bob dostane
náhodou správný výsledek. Zbývá ale 25 % pravděpodobnost, že kvůli Evinu měření dostane Bob jiný výsledek.
Čím více bitů Alice a Bob veřejně porovnají, tím méně jich mohou použít pro samotné širování, ale Evě tím
více komplikují život. Při n porovnaných bitech je pravděpodobnost 1−(3/4)n,
že Eva bude odhalena. Už při 32 bitech je to 99,99 %.
|

a) Alice generuje náhodné bity.
b) Alice náhodně volí báze.
c) Alice kóduje bity do polarizace fotonů a odesílá je Bobovi.
d) Bob náhodně volí báze.
e) Bob v nich měří přijaté fotony.
f) Bob dekóduje bity.
g) Alice a Bob se veřejně domluví, na kterých bázích se shodli.
h) Alice a Bob obětují některé bity na detekci odposlechu.
i) Všechny kontrolované bity se shodují, takže Eva neposlouchá.
j) Zbylé bity tvoří tajný klíč pro Vernamovu šifru.
|
Příklad výměny klíče podle protokolu BB84
Spolehlivost metody
Je tento postup vážně zcela spolehlivý? První problém, který Vás možná napadne, spočívá v zahození klíče
v bodě 6. Znamená to, že pokud Eva na lince vytrvale odposlouchává, nemůže se Alice s Bobem na klíči nikdy
dohodnout. To je ale problém spíše technický než kryptografický – nepřítel může přerušit komunikační
kanál třeba i fyzickým zásahem a kryptografický protokol s tím nic nenadělá. Horší je, že mnohonásobné
opakování uvedeného postupu zvyšuje Evinu nepatrnou šanci, že jednou jí odposlech projde. Je proto nutné
mít dostatek kontrolních bitů.
Existuje ale i větší problém: Protokol nijak neřeší autentizaciAutentizace – ověření totožnosti osoby, s níž komunikujeme.
na veřejném kanále. Jestliže Bob například
v bodě 5 sděluje něco veřejně Alici, ta si nemusí být jista, zda mluví skutečně s Bobem a ne Evou. To Evě
umožnuje zcela převzít Bobovu roli a získat od Alice tajné informace místo Boba. Protokol kvantové kryptografieKryptografie
– věda zabývající se utajováním smyslu zpráv převodem do podoby, která
je čitelná jen se speciální znalostí. Slovo pochází z řečtiny: kryptós je skrytý a gráphein
znamená psát. Někdy je pojem obecněji používán pro vědu o čemkoli
spojeném se šiframi a je alternativou k pojmu kryptologie.
tuto otázku neřeší, autentizaceAutentizace – ověření totožnosti osoby, s níž komunikujeme.
není jeho součástí, a může se proto stát slabým místem
konkrétní realizace.
Systém kvantové kryptografieKryptografie
– věda zabývající se utajováním smyslu zpráv převodem do podoby, která
je čitelná jen se speciální znalostí. Slovo pochází z řečtiny: kryptós je skrytý a gráphein
znamená psát. Někdy je pojem obecněji používán pro vědu o čemkoli
spojeném se šiframi a je alternativou k pojmu kryptologie.
poprvé v laboratoři vyzkoušeli Charles Bennett a John Smolin v roce 1989.
Od té doby byla vymyšlena řada technických zlepšení a princip postupně přešel v technologii. Dnes už je
možné systém kvantové kryptografie získat ryze komerční cestou, i když je to drahá záležitost a přenos je
pomalý. K přenosu fotonů slouží optická vlákna. K měření polarizacePolarizace fotonu
– rovina kmitů elektrického pole, fotony jako kvanta příčného
elektromagnetického vlnění mohou mít dvě nezávislé polarizace. Skutečný
stav fotonu je potom lineární kombinací obou polarizačních stavů
v dané bázi.
se používá krystal CaCO3,
kterým foton buď projde rovně nebo se z původního směru odkloní. Práce s jednotlivými fotony je
problematická hlavně při větší vzdálenosti uživatelů, protože je vyloučeno použití zesilovačů. Rekordní
vzdálenost je dnes 122 kilometrů s použitím standardního optického vlákna. Rychlost většinou nepřesahuje
2 kbit/s.

První systém kvantové kryptografie. Kvantový kanál je dlouhý 30 cm.
Zdroj: J. A. Smolin, IBM Thomas J. Watson Research Center.
V souvislosti s kvantovou kryptografií se dostal do popředí pojem nepodmíněná bezpečnost. Značí, že
bezpečnost komunikace není podmíněna žádnými předpoklady na schopnosti a technické možnosti útočníka.
Bezpečnost dosud nejčastěji používaných kryptografických systémů je založena na výpočetní složitosti
čili na faktu, že nejsou známy dostatečně rychlé postupy a dostatečně výkonné počítače na vyřešení
určitých úloh. Kvantová kryptografie žádné takové předpoklady neobsahuje. Ani síla kvantových počítačů
ani jakýchkoliv jiných systémů nemůže porušit přírodní zákony, o které se tento systém opírá. Je tu
jediný tichý předpoklad, že pro Alici, Boba i pro Evu platí zákony kvantové mechaniky. To není docela
samozřejmé, neboť víme, že standardní modelStandardní model
– jedná se o standardní model elementárních částic (leptonů
a kvarků), které interagují prostřednictvím elektromagnetické,
slabé a silné interakce. Interakčními částicemi jsou fotony,
intermediální bosony Z, W+ a W− a gluony. Součástí teorie jsou dosud neobjevené Higgsovy bosony způsobující narušení symetrie v teorii.
nepopisuje všechny aspekty fyzikální reality. Teorie všehoTeorie všeho
– konzistentní popis všech základních přírodních sil a hmoty v jednom
rámci. Tento cíl teoretické fyziky vytyčil Albert Einstein, doposud
však nebyl dosažen. Nadějným kandidátem je M-teorie (teorie superstrun).
ještě nebyla nalezena a může se ukázat, že platnost dnes známých přírodních zákonů má své meze. Přesto
lze předpoklad platnosti kvantové mechaniky považovat za rozumný. Je to dosud nejpřesněji ověřená
fyzikální teorie všech dob a máloco na světě je tak spolehlivé jako přírodní zákony.
Báseň o kvantové kryptografii
Autor: John Preskill
Alice said to her friend Eve,
"Why do you practice to deceive?
You know I need to talk to Bob.
Without that I won't have a job.
"Bob can't know where my note has been.
He thinks that you are listening in.
He wonders if it's safe enough
For me to send him secret stuff.
"And Bob's right not to trust you, Eve,
With quantum tricks stuffed up your sleeve.
But he thinks we can freeze you out,
With quantum tricks we've learned about.
"With quantum states, what we achieve
Defeats whatever you conceive.
So even Bob has to believe
That you can't hear us, can you Eve?"
|
Bonus: Kvantová kryptografie
Na klipu můžete vidět základní postup kvantové kryptografie až po získání
klíče. Popisky jednotlivých kroků jsou v angličtině, ale kopírují zde uvedený
článek. Animaci také můžete spustit ve formátu
flash.
Odkazy

|
|